系统梳理：杨-米尔斯理论的数学结构

——————

杨-米尔斯理论的数学结构是“几何-拓扑-代数”三位一体：

几何层把场诠释为主丛联络；拓扑层用瞬子与示性类刻画非微扰扇区；代数层用 L∞-或微分分次李代数统一编码对称性与方程。

三者的交叉不仅为标准模型的量子计算提供严格框架，也反向推动了四维拓扑、复几何与范畴论的发展。

一、几何语言：主丛-联络-曲率

1. 主丛 P(M,G)

底流形 M（一般取 4 维洛伦兹或欧氏时空）。

结构群 G⊂U(n) 为紧致李群，对应物理上的色对称群。

2. 联络 1-形式 ω∈Ω¹(P,g)

局部平凡化下拉回给出规范势 A=sω，对应物理上的胶子场。

规范变换等价于不同局部截面之间的过渡函数 u:M→G 的主动变换：

A↦u⁻¹Au+u⁻¹du

3. 曲率 2-形式 F=dA+A∧A

满足比安基恒等式 DAF=0（几何恒等式）。

杨-米尔斯方程 DAF=0（变分运动方程）。

4. 作用量泛函

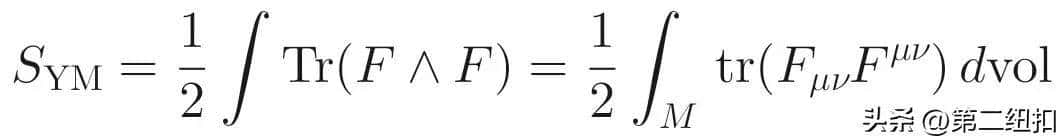
其临界点即杨-米尔斯方程；几何上对应“杨-米尔斯联络”——使 L²-范数曲率取极值的联络。

二、拓扑与瞬子

1. 第二陈类/庞特里亚金数

k=1/(8π²)∫Tr(F∧F)∈ℤ

把四维流形上的规范场按整数 k 分类，称瞬子数。

2. 瞬子解

欧氏空间中自对偶 F=F（或反自对偶 F=−F）的有限作用量解。

模空间 _k 维数=8k−3，携带自然超凯勒度量，是 Donaldson 理论的基石。

3. 拓扑量子场论嵌入

通过 BFYM 或 TYM 的场重定义，可把纯杨-米尔斯作用量拆成“拓扑项+量子涨落”，瞬子贡献表现为非微扰隧穿效应。

三、代数视角：L∞-代数与同源

1. 将规范场 A∈Ω¹(M,g) 放入分次向量空间

V=Ω⁰⊕Ω¹⊕Ω^{d−1}⊕Ω^d，

赋予高阶括号 ℓ₁,ℓ₂,ℓ₃，使得杨-米尔斯作用量写成同伦李代数意义下的“同源作用量”：

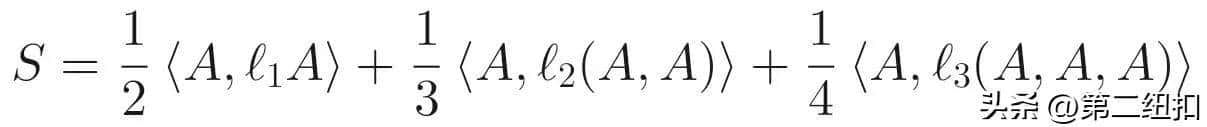
2. 该 L∞-代数编码了规范对称性、场方程与诺特恒等式的全部信息，为 BV-BRST 量子化提供代数骨架。

四、超对称与复几何

1. 最大超对称杨-米尔斯可置于复化超平移群商空间 R 上。

2. 把规范势组合成 (0,1)-型联络 ω，则杨-米尔斯方程等价于 Maurer-Cartan 方程

∂̄ω+ω∧ω=0

从而把解空间刻画为某种全纯向量丛的模空间。

五、分析与模空间

1. Uhlenbeck 紧化：

在四维情形下，对连接序列 {A_i} 若 ∫|F|²≤Λ，则存在“气泡”极限，保证模空间在扣去可去奇点后紧。

2. Sobolev 完备化：

取 A∈H¹,²(M,TM⊗g)，G⊂H²,²(M,G)，可在商空间 =A/G 上定义局部坐标与黎曼度量，为研究质量 gap、谱几何提供分析基础。

六、现代交叉前沿

1. Donaldson–Witten 不变量：

用 _k 的拓扑数据定义四维光滑流形微分不变量，揭示四维独有的“ exotic ℝ⁴”现象。

2. AdS/CFT 与全息：

四维 N=4 超杨-米尔斯对应十维 IIB 弦在 AdS₅×S⁵ 背景，为研究强耦合 gauge 理论提供可计算框架。

3. 非交换与编织对称：

把时空坐标非交换化后，规范群推广至量子群，L∞-代数结构仍保持，仅修改括号与霍奇算子，给出非交换杨-米尔斯的一致定义。