融合 K-means与DTW时间序列聚类！！

内容分享3小时前发布 L-yun珍

0 0 0

哈喽，我是小白~

今儿和大家聊：混合K-means与DTW的时间序列聚类。

DTW对齐时间序列的非线性变速特性，提升了类似性度量的准确性。K-means结合DTW，能够高效地聚类复杂的时间序列模式，适应不同步或变速数据。这种结合广泛应用于金融、医疗等领域，但计算复杂度较高，需要优化策略支持大规模数据处理。

关注了吗？每一篇都是干货 满满满满！~

咱们先从理论聊起~

理论与原理

核心思想

时间序列聚类是分析和处理时间序列数据的重大方法。时间序列数据一般具有时间依赖性和高维性，传统的欧几里得距离（Euclidean Distance）在捕捉时间序列形态类似性方面存在局限。因此：

DTW（动态时间规整） 被引入，它是一种非线性对齐技术，可以有效计算时间序列之间的最小距离，即使序列在时间轴上有局部伸缩或移动。
K-means 聚类 是一种简单、高效的非监督学习算法，利用数据点之间的距离关系进行分组。

「混合 K-means 与 DTW」结合了二者的优势：

使用 DTW 作为距离度量，能捕捉时间序列的形状类似性。
利用 K-means 的中心点更新规则，使得聚类过程高效且适用于大规模数据。

核心原理

设时间序列数据集为，每个是长度为的时间序列。混合 K-means 与 DTW 的流程包括以下步骤：

1. 初始聚类中心选择 ：

随机选择个时间序列作为初始聚类中心。

2. 距离计算 ：

使用 DTW 计算样本到每个中心的距离：

其中表明时间序列对齐路径。

3. 分配样本 ：

将每个样本分配到与其最近的聚类中心：

4. 更新聚类中心 ：

对每个聚类计算新的中心序列，可通过所有成员序列的动态平均路径计算获得：

5. 迭代 ：

重复步骤 2-4，直至中心点变化小于预设阈值或达到最大迭代次数。

优势与适用场景

优势：

适合具有时间依赖特性的高维数据。
DTW 可处理时间序列的局部时间伸缩，增强了聚类的鲁棒性。

适用场景 ：

生物信号分析（如心电图）。
金融时间序列建模。
物联网传感器数据。

特殊注意事项

DTW 的计算复杂度较高，对大规模数据需优化实现（如多线程或降维）。
时间序列的归一化处理可提高聚类效果。
初始聚类中心选择对最终结果影响较大，可用 K-means++ 初始化策略。

案例展示

我们以虚拟数据集为例，包含 4 类时间序列数据（如传感器温度读数），展示混合 K-means 与 DTW 的实际应用。

数据生成及预处理

importnumpyasnp
importmatplotlib.pyplotasplt
fromscipy.cluster.hierarchyimportdendrogram
fromtslearn.clusteringimportTimeSeriesKMeans
fromtslearn.metricsimportdtw
fromtslearn.preprocessingimportTimeSeriesScalerMeanVariance

# 数据生成
np.random.seed(42)
n_samples, n_timestamps =100,50
cluster_1 = np.sin(np.linspace(0,4* np.pi, n_timestamps)) + np.random.normal(0,0.1, (25, n_timestamps))
cluster_2 = np.cos(np.linspace(0,4* np.pi, n_timestamps)) + np.random.normal(0,0.1, (25, n_timestamps))
cluster_3 = np.sin(np.linspace(0,8* np.pi, n_timestamps)) + np.random.normal(0,0.1, (25, n_timestamps))
cluster_4 = np.cos(np.linspace(0,8* np.pi, n_timestamps)) + np.random.normal(0,0.1, (25, n_timestamps))

data = np.vstack([cluster_1, cluster_2, cluster_3, cluster_4])

# 数据归一化
scaler = TimeSeriesScalerMeanVariance
data_scaled = scaler.fit_transform(data)

模型构建与训练

# 构建 K-means 模型
model = TimeSeriesKMeans(n_clusters=4, metric="dtw", max_iter=50, random_state=42)
y_pred = model.fit_predict(data_scaled)

# 获取聚类中心
centroids = model.cluster_centers_

图形分析与解释

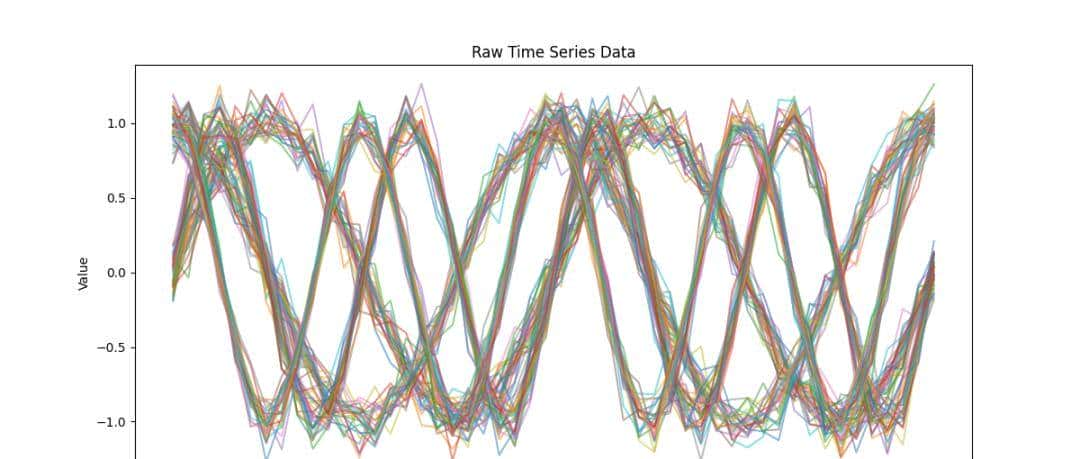
1. 原始数据分布 ：展示不同时间序列的原始特性。

plt.figure(figsize=(12,6))
fori, clusterinenumerate([cluster_1, cluster_2, cluster_3, cluster_4],1):
forseriesincluster:
plt.plot(series, alpha=0.5)
plt.title("Raw Time Series Data")
plt.xlabel("Time")
plt.ylabel("Value")
plt.show

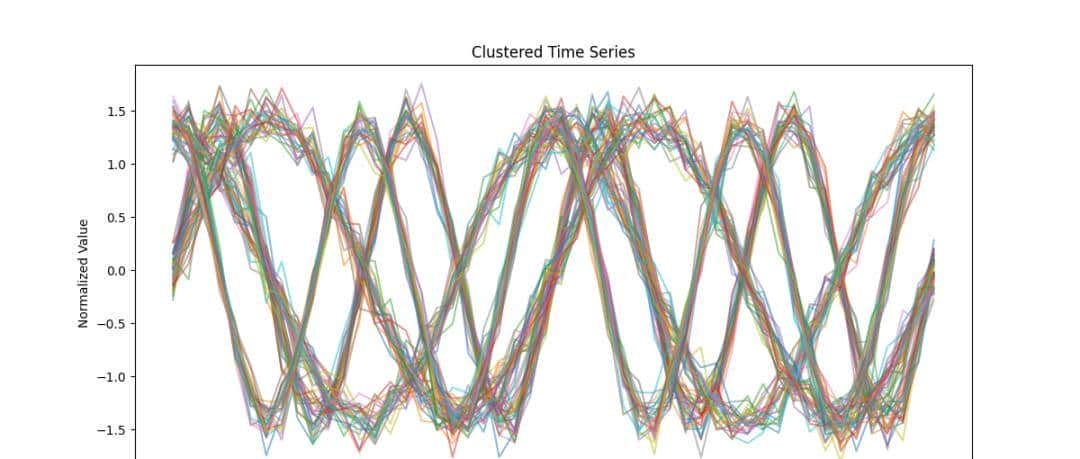
融合 K-means与DTW时间序列聚类！！

2. 聚类结果展示 ：每个类的时间序列用不同颜色标识。

plt.figure(figsize=(12,6))
forcluster_idxinrange(4):
cluster_data = data_scaled[y_pred == cluster_idx]
forseriesincluster_data:
plt.plot(series.flatten, alpha=0.5)
plt.title("Clustered Time Series")
plt.xlabel("Time")
plt.ylabel("Normalized Value")
plt.show

融合 K-means与DTW时间序列聚类！！

3. 聚类中心对比 ：展示每个聚类的代表性。

plt.figure(figsize=(12,6))
fori, centroidinenumerate(centroids):
plt.plot(centroid.flatten, label=f"Cluster{i+1}")
plt.title("Cluster Centers")
plt.xlabel("Time")
plt.ylabel("Normalized Value")
plt.legend
plt.show

4. 聚类性能评估 ：通过动态时间规整距离矩阵进行热力图分析。

fromtslearn.metricsimportcdist_dtw

dist_matrix = cdist_dtw(data_scaled)
plt.figure(figsize=(8,8))
plt.imshow(dist_matrix, cmap='hot', interpolation='nearest')
plt.title("DTW Distance Heatmap")
plt.colorbar
plt.show