序参量：理解连续相变、对称破缺和系统宏观秩序的关键概念

“序参量”最早由朗道引入热力学，后被哈肯推广到协同学，现已成为统计物理、凝聚态、化学、生物乃至社会系统建模的通用语言。

它是“对称破缺的指针、多体问题的降维器”。

正确选取它=“对称性+慢模+可测”

正确计算它=“严格零检查+标度律+有限尺寸外推”

一句话：

将上千个自由度的复杂系统装进一个简洁的序参量方程，看清相变、同步与自组织的本质。

一、背景：为什么需要序参量

1. 连续相变没有潜热和两相共存，传统热力学变量（P、T、ρ）无法标记“有序-无序”转变。

2. 朗道 1937 年提出：

只要系统发生自发对称破缺，就存在一个宏观变量 ψ，它在高温（高对称）相恒为零，在低温（低对称）相非零，这就是序参量。

3. 哈肯 1970 年代把同一思想搬到协同学：

大量子系统通过非线性耦合产生宏观合作模式，合作模式的幅值就是序参量，它反过来“役使”子系统行为，实现降维描述。

二、作用：

一句话——“把对称破缺可视化，把多体问题降维”

1. 标记相变：

ψ=0 ↔ 无序相；

ψ≠0 ↔ 有序相。

2. 量化对称破缺程度：

|ψ|∈[0,1] 越大，有序度越高。

3. 给出临界行为：

ψ∼|t|^β，

t=(T–T_c)/T_c，

β 是普适临界指数。

4. 役使原理（Slaving Principle）：

在临界区，所有慢模（Goldstone 模、守恒量）都被序参量场驱动，数学上可把上千个微观自由度投影到一两个序参量方程，如

∂ψ/∂t = aψ – b|ψ|²ψ + D∇²ψ + η(x,t)

5. 跨学科迁移：

激光光强、化学反应坐标、胚胎形态主轴、社会舆论极化率，都可写成同一类序参量方程，实现“异质同构”建模。

三、如何正确选取与计算

1. 选取原则（“艺术”部分）

a) 对称性：

ψ 必须按破缺对称群的不可约表明变换。

b) 守恒律：

不能与被保留的对称性冲突。

c) 可观测：

能被实验或模拟直接测量。

d) 慢模：

弛豫时间最长，其它模可绝热消去。

例：

铁磁体：M = 〈Σ_i s_i〉/N，总磁化强度。

向列液晶：S = 〈P₂(cosθ)〉= ½〈3cos²θ–1〉，θ 为分子长轴与指向矢夹角。

黄铜有序-无序：ψ = (R–W)/(R+W)，R、W 为正确/错误占位原子数。

Kuramoto 同步：Z₁ = (1/N)Σ_j e^{iθ_j}，|Z₁| 即相干因子。

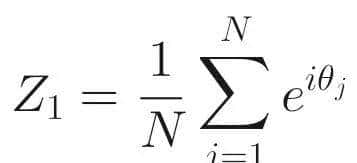
2. 计算步骤（“技术”部分）

① 确定破缺的对称群 G→H。

② 列出所有 G 下不变、H 下非零的最低维表明，构造候选 ψ。

③ 用 Monte-Carlo、分子动力学或密度矩阵对角化，计算候选量的热力学平均。

④ 检查：

在 T_c 以上是否严格为零（有限尺寸下用 Binder cumulant 或分布双峰法外推）。

临界区是否满足标度律 χ∼|t|^{–γ}，C∼|t|^{–α}，且 β,γ,α 与普适类一致。

⑤ 若多个候选量同时非零，选弛豫最慢、与外部场共轭的那个。

3. 有限尺寸与误差控制

系统太小：ψ 会因涨落“假非零”，用 Binder 比

U_L = 1 – 〈ψ⁴〉/(3〈ψ²〉²)

交叉点定 T_c。

统计不足：临界慢化导致自相关时间 τ∼L^z，需并行回火或集群算法。

外场耦合：测量磁化曲线时，外场 h 必须小到 |h|≪|t|^{βδ}，否则把临界行为掩盖。

四、常见误区与检查清单

1. 把“序参量”当“有序度”：

序参量是一个场量，可正可负，可空间调制；有序度一般是其平均值或绝对值。

2. 忽略 Goldstone 模：

连续对称破缺时，ψ 的相位涨落发散，需用刚性指数 ρ_s 或超流密度表征长程序。

3. 一级相变也硬凑 ψ：

一级相变有两相共存，ψ 在共存区双稳，不能简单幂律拟合。

4. 高阶项乱截断：

朗道自由能展开 F = aψ² + bψ⁴ + cψ⁶，若 b<0 需保留六次项，否则得到非物理的一级相变。

5. 非平衡过程张冠李戴：

化学反应、生物形态发生是非平衡，ψ 可定义，但临界指数不必定与平衡普适类一样，需用驱动-耗散场论重正化群处理。