泰勒展开式作为高等数学中的“万能工具”,常常让许多同学觉得“抽象难懂、用不上手”,但实际上,它在极限计算、不等式证明、导数应用等高频习题中有着“化繁为简”的神奇效果。掌握泰勒展开式的核心应用技巧,能让你在面对复杂习题时快速破题,效率翻倍!
一、泰勒展开式核心公式(必背基础)
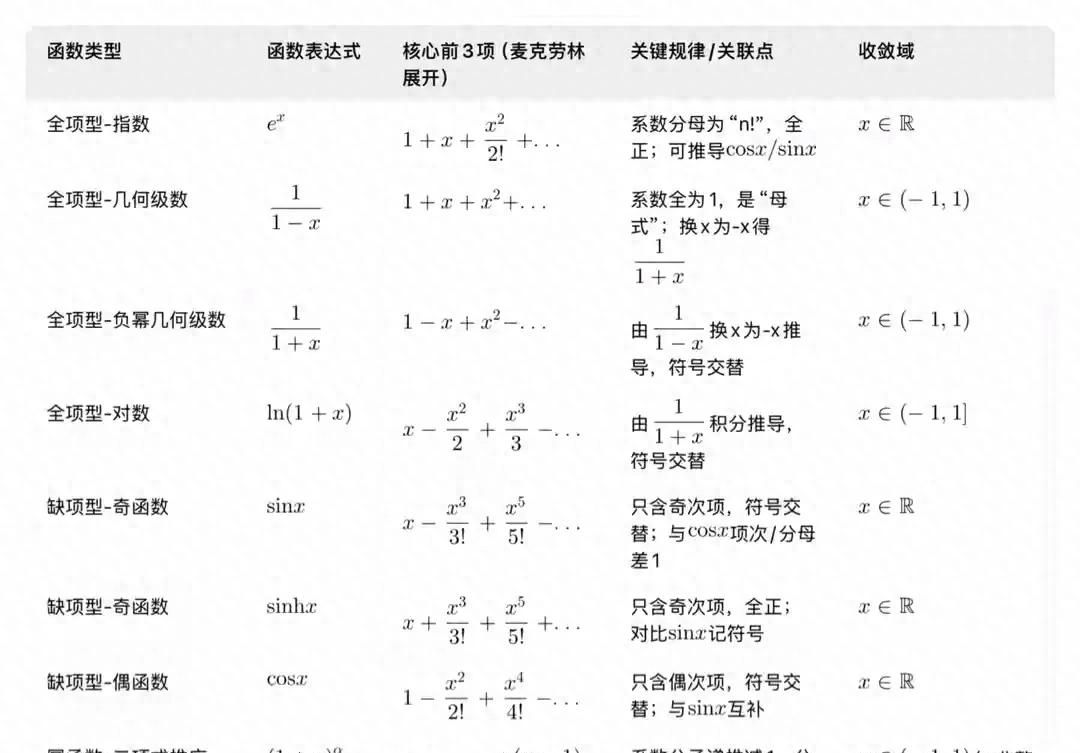
泰勒展开式的本质是“用多项式逼近复杂函数”,在习题中最常用的是 麦克劳林展开式(泰勒展开式在x=0处的特殊形式),记住以下5个高频函数的展开式,就能应对80%的习题:
1. eˣ = 1 + x + x²/2! + x³/3! +… + xⁿ/n! + o(xⁿ)
2. ln(1+x) = x – x²/2 + x³/3 – x⁴/4 +… + (-1)ⁿ⁺¹xⁿ/n + o(xⁿ)(x∈(-1,1])
3. sinx = x – x³/3! + x⁵/5! -… + (-1)ⁿx²ⁿ⁺¹/(2n+1)! + o(x²ⁿ⁺¹)
4. cosx = 1 – x²/2! + x⁴/4! -… + (-1)ⁿx²ⁿ/(2n)! + o(x²ⁿ)
5. (1+x)ᵃ = 1 + ax + a(a-1)x²/2! +… + a(a-1)…(a-n+1)xⁿ/n! + o(xⁿ)(a为实数)
关键原则:展开到“与分母同阶”或“消去低阶项”即可,无需展开过多项,避免计算繁琐。
二、泰勒展开式3大高频习题应用场景
场景1:极限计算(秒杀复杂0/0型、∞/∞型极限)
当遇到含eˣ、ln(1+x)、sinx等函数的极限,尤其是“等价无穷小替换失效”的情况,泰勒展开式能精准破解。
例题:求极限 lim(x→0) [eˣ – (1 + x + x²/2)] / x³
常规方法:洛必达法则(需求导3次,步骤繁琐)
泰勒展开法(秒解):
1. 由eˣ的麦克劳林展开式,展开到x³项:eˣ = 1 + x + x²/2! + x³/3! + o(x³)
2. 代入分子:eˣ – (1 + x + x²/2) = (1 + x + x²/2 + x³/6 + o(x³)) – (1 + x + x²/2) = x³/6 + o(x³)
3. 计算极限:lim(x→0) [x³/6 + o(x³)] / x³ = 1/6
优势:跳过多次求导,1分钟出结果,避免求导失误。
场景2:不等式证明(轻松处理含高阶导数的不等式)
当题目给出“函数高阶导数有界”或“需证明函数与多项式的大小关系”时,泰勒展开式结合拉格朗日余项,能快速建立不等式。
例题:证明当x>0时,ln(1+x) < x – x²/2 + x³/3
泰勒展开法(秒解):
1. 对ln(1+x)在x=0处展开,取拉格朗日余项(展开到x³项):
ln(1+x) = x – x²/2 + x³/3 – x⁴/(4(1+ξ)⁴)(其中0<ξ<x)
2. 分析余项:x>0时,-x⁴/(4(1+ξ)⁴) < 0(余项为负)
3. 整理得:ln(1+x) = [x – x²/2 + x³/3] + (负数) < x – x²/2 + x³/3,不等式得证。
优势:直接关联函数与多项式,无需构造复杂辅助函数。
场景3:导数应用(求函数的高阶导数、近似计算)
泰勒展开式可快速求函数在某点的高阶导数值,还能用于近似计算,是导数应用题的“捷径”。
例题1:求高阶导数:求f(x)=eˣ在x=0处的5阶导数f⁽⁵⁾(0)
泰勒展开法:
由eˣ = 1 + x + x²/2! + x³/3! + x⁴/4! + x⁵/5! + o(x⁵),根据泰勒展开式系数与高阶导数的关系:
f⁽ⁿ⁾(0)/n! = 展开式中xⁿ的系数,故f⁽⁵⁾(0)/5! = 1/5! → f⁽⁵⁾(0) = 1。
例题2:近似计算:近似计算sin1°(准确到10⁻⁵)
泰勒展开法:
1. 转化为弧度:1° = π/180 ≈ 0.0174533弧度
2. sinx ≈ x – x³/3!(x很小时,高阶项可忽略)
3. 代入计算:sin(π/180) ≈ 0.0174533 – (0.0174533)³/6 ≈ 0.0174524,误差小于10⁻⁵。
三、泰勒展开式应用核心技巧(避坑指南)
1. “同阶原则”:极限计算中,分子分母展开到“同阶无穷小”即可,列如分母是x³,分子展开到x³项,高阶无穷小o(x³)可直接忽略;
2. “余项选择”:证明不等式用“拉格朗日余项”(带具体误差项),极限计算用“佩亚诺余项”(o(xⁿ),简洁方便);
3. “优先展开高频函数”:遇到eˣ、ln(1+x)、sinx、cosx,优先用泰勒展开,比洛必达、等价替换更高效。
总结:泰勒展开式——习题中的“破题神器”
泰勒展开式看似抽象,实则是解决复杂高数习题的“捷径”:极限计算中秒杀“洛必达多次求导”,不等式证明中避开“构造辅助函数”,导数应用中快速求高阶导数。只要记住核心展开式,掌握“同阶展开、按需选余项”的技巧,就能轻松应对各类习题,让高数解题更高效、更精准!













收藏了,感谢分享