多元函数泰勒公式

泰勒公式是一个超级重大的数学工具，无论是物理学、工程学、经济学，泰勒公式都发挥着重大的作用。泰勒公式的含义是将任意一个光滑函数在某一点处展开成多项式的表达式，通过使用泰勒公式可以近似描述物理过程、优化机械系统、分析经济变量、实现数字求解器等，所以泰勒公式在科学研究和技术应用中价值都超级高。信任大家对于一元函数的泰勒公式应该不陌生，而多元函数泰勒公式与一元函数泰勒公式相仿，作用和意义也是一样的，但由于多元函数更加复杂，所以二者之间也不尽一样，而且大家对它可能没有那么熟悉。本文重点讲解二元函数泰勒公式，为了便于理解，以二元函数为例，介绍多元函数泰勒公式，希望对大家有所协助。

一、一元函数泰勒公式

第一回顾一元函数泰勒公式。若f(x)在包含x0的某开区间(a，b)内具有直到n+1阶的导数，则当x∈(a，b)时，将下式称为泰勒公式：

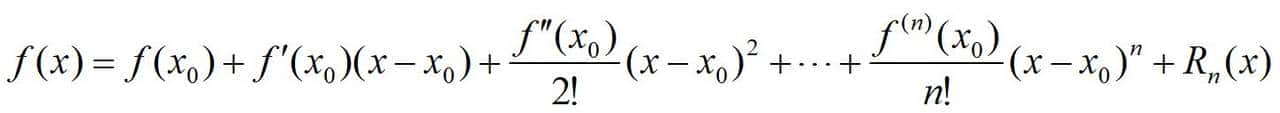
一元函数泰勒公式

拉格朗日余项

ξ在x0与x之间，称为n阶泰勒公式的拉格朗日余项；若：

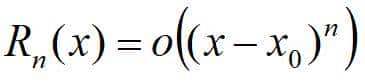
佩亚诺余项

则称为佩亚诺余项。若在泰勒公式中取x0=0，则称之为麦克劳林公式。

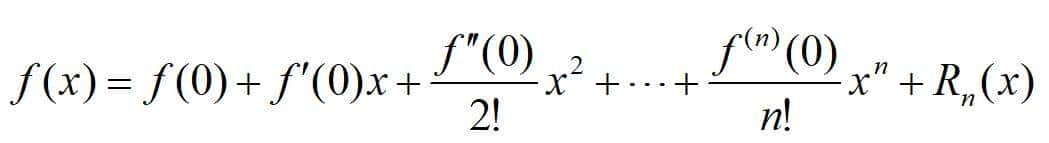
麦克劳林公式

为了方便后面的记号，令h=x-x0，泰勒公式可重新记作如下形式：

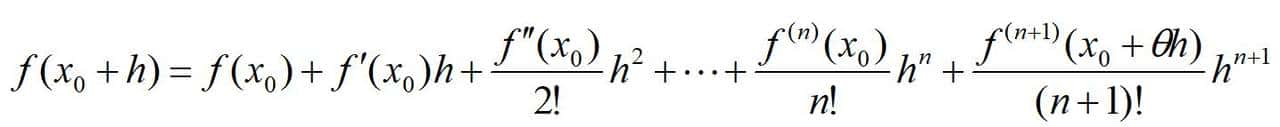
θ∈(0,1)

注意：令x0=a,x0+h=b，只取泰勒公式的第一项，即：

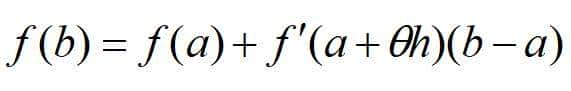
一元函数的拉格朗日中值公式

上式即为一元函数的拉格朗日中值公式。

二、二元函数泰勒公式

类似于一元函数，多元函数泰勒公式的基本思想也是：在某点附件，如何将一个函数表明为多元多项式的形式。下面以二元函数为例，给出相应的泰勒公式。

设二元函数z=f(x,y)在点(x0,y0)的某邻域具有直到n+1阶连续偏导数，(x0+h,y0+k)为该邻域的任意一点，则有：

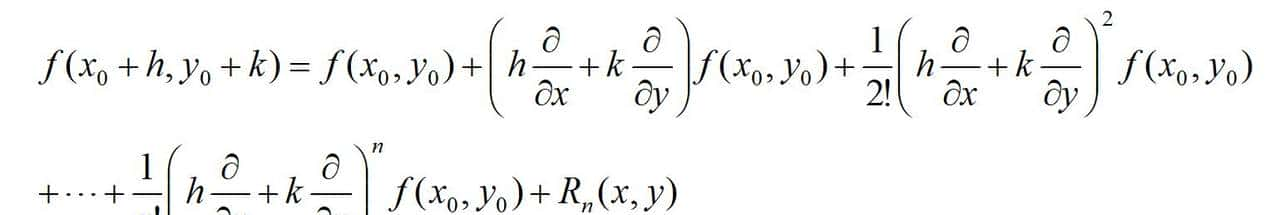
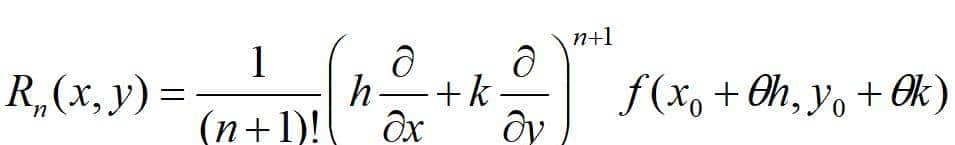
θ∈(0,1)

式中:

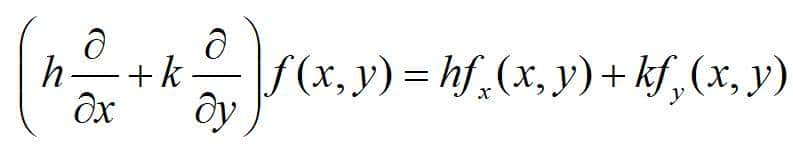
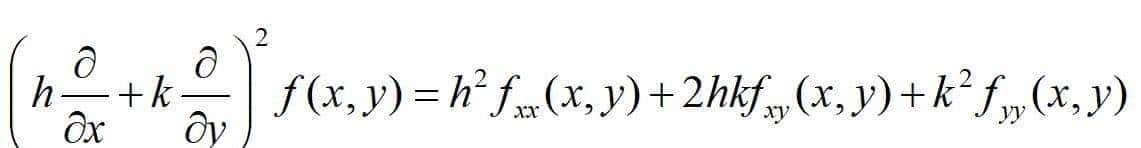
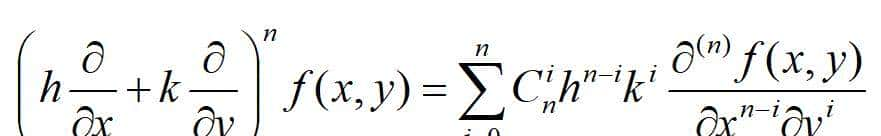
目前对二元泰勒公式给予证明：

对于邻域内给定的点(x0+h,y0+k)，引入如下的辅助函数：

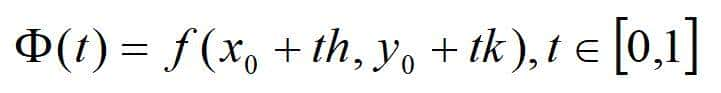
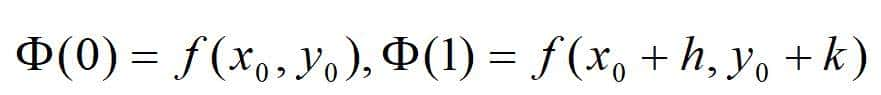
函数Φ(t)在区间[0,1]上满足一元函数泰勒定理的条件，于是有：

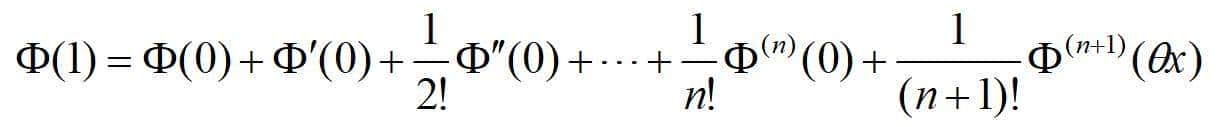
θ∈(0,1)

根据二元复合函数的求导法则可得：

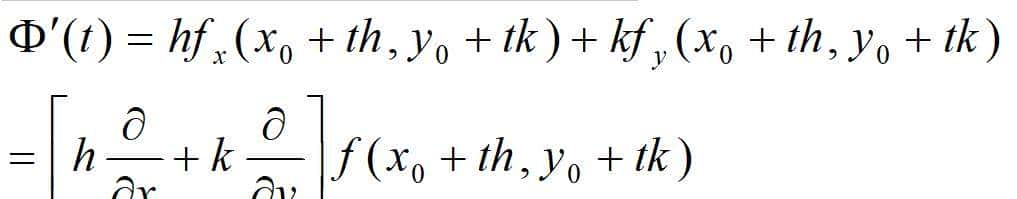
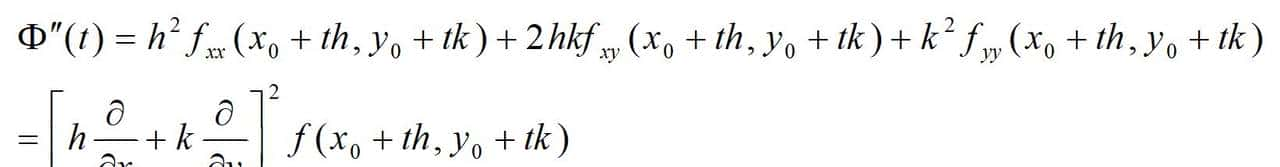
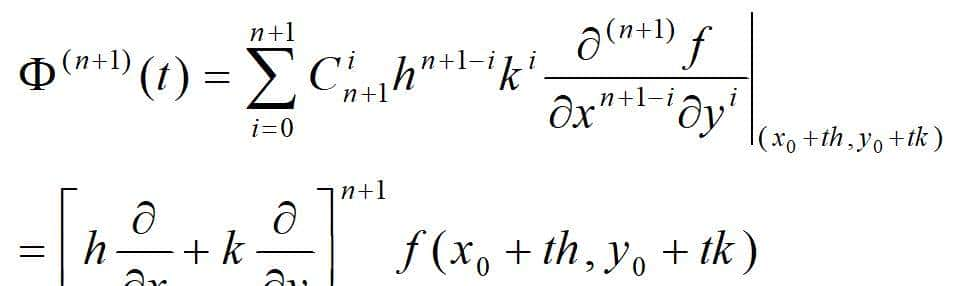
在前面的表达式中，令t=0，便可以得到Φ(t)直到n阶导数在(x0,y0)的值，并将在t=θ

的值代入到表达式：

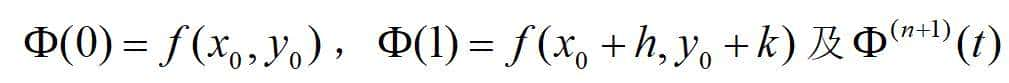
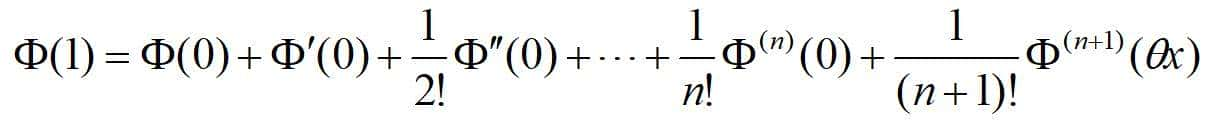
便可得到二元函数带拉格朗日余项的n阶泰勒公式。

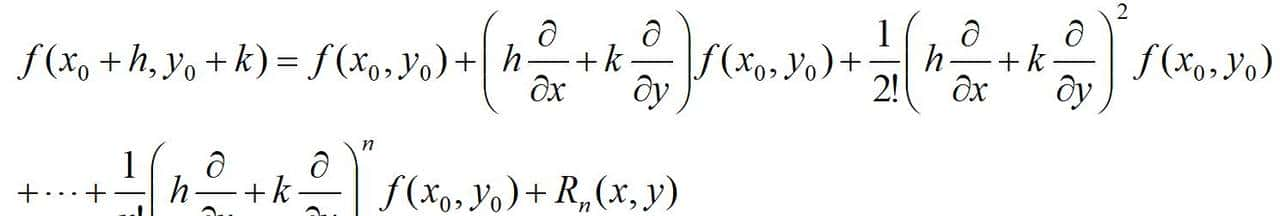
二元函数的n阶泰勒公式

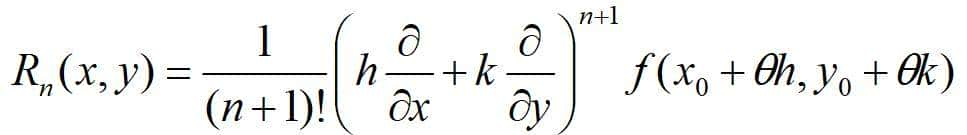
拉格朗日余项，θ∈(0,1)

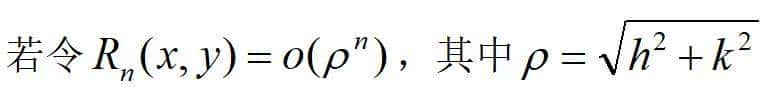
佩亚诺余项

即可得到带有佩亚诺余项的n阶泰勒公式。

若令(x0，y0)=(0,0)，便可得到带有拉格朗日余项的n阶麦克劳林公式：

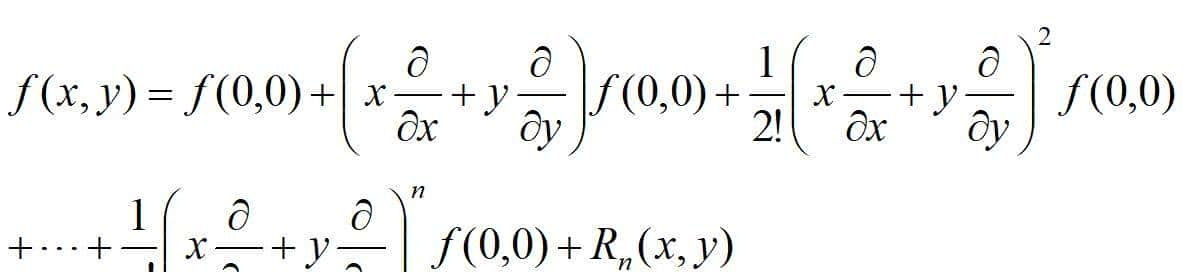
二元函数麦克劳林公式

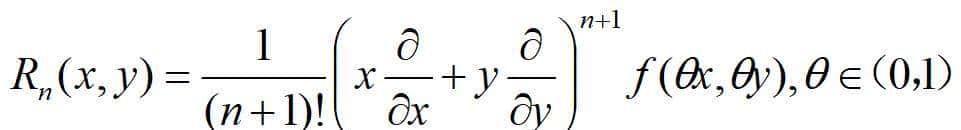
特别地，同一元函数泰勒公式一样，若只取二元函数泰勒公式的第一项，即：

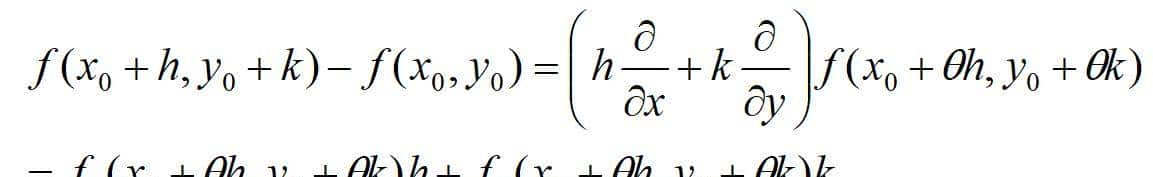
二元函数的中值公式

上式即为二元函数的中值公式。

对于多元函数泰勒公式暂时介绍到这，希望对你有所协助。