CSS3 transform Matrix

内容分享2天前发布家养Karry喵

0 0 0

之前大家在CSS3 动画里用到比较多的transform属性，实际上transform属性的好多方法都是可以通过matrix实现的效果。本文以2D效果举例。

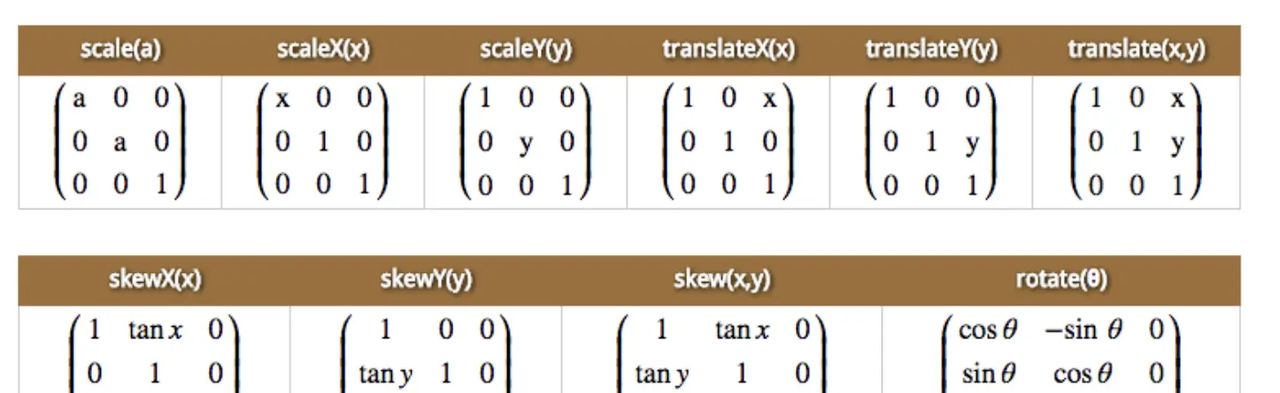
1、 transform属性

包括几个常用方法

skew (斜拉)
scale (缩放)
rotate (旋转)
translate (位移)

上面的几种方法都是应用matrix()方法实现的

2、matrix方法

用法

transform: matrix(a,b,c,d,e,f);

实际上对应的矩阵是

CSS3 transform Matrix

以上矩阵中的1，是2D矩阵不涉及Z轴，所以将Z轴置常数1

转换的公式如下

CSS3 transform Matrix

其中x, y表明转换元素的坐标（变量), 运用的是线性代数矩阵的乘法，可以得出转换后的坐标了。

举例设置

transform: matrix(1, 0, 0, 1, 100, 100);

效果就是往右平移100px的同时往下也平移了100px

3、matrix矩阵实现缩放，旋转以及拉伸

推导rotate(βdeg)

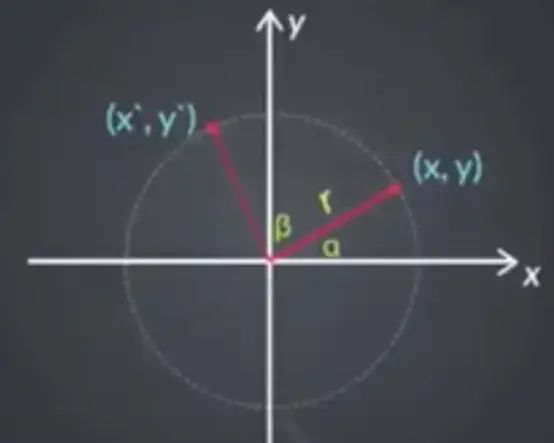
CSS3 transform Matrix

# 由(x,y)旋转到(x ,y  )
x  = cos(β+α)*r
y  = sin(β+α)*r

已知公式：
r = √x^2+y^2

和差化积公式：
sin(β+α)= sin(β)cos(α) + cos(β)sin(α)
cos(β+α) = cos(β)cos(α) - sin(β)sin(α)

正弦余弦
sin(α) = y/r
cos(α) = x/r

所以得到
x  = cos(β+α)*r = cos(β)cos(α)r-sin(β)sin(α)*r    = cos(β)x - sin(β)y
y  = sin(β+α)*r = sin(β)*cos(α)*r+cos(β)sin(α)*r  = sin(β)x + cos(β)y

整理出矩阵如下
|cos(β)    - sin(β)  |  * | x |     =   | x |
| sin(β)    cos(β)   |    | y |         | y |

上面matrix矩阵中的参数分别为
a 水平缩放
b 水平拉伸
c 垂直拉伸
d 垂直缩放
e 水平位移
f 垂直位移
实现默认方法的矩阵可以由必定的数学推导得出

缩放：scale(a) 等同于 matrix(a, 0, 0, a, 0, 0);
平移：translate(m, n) 等同于 matrix(1, 0, 0, 1, m, n);
旋转：rotate(ndeg) 等同于 matrix(cos(ndeg), sin(ndeg), -sin(ndeg), cos(ndeg), 0, 0);
拉伸：skew(mdeg, ndeg) 等同于 matrix(1, tan(ndeg), tan(mdeg), 1, 0, 0);

矩阵的优势是可以通过计算，然后将平移旋转等效果整合到一个表达式内。
列如 transform: skewX(45deg) scale(1.2);

换成矩阵

CSS3 transform Matrix

最后我们只需要设置 transform: matrix(1.2,0,1.2,1.2,0,0);

4、用处

虽然有了matrix转换矩阵,但是日常中直接使用提供出来的translate, rotate等方法比较方便，这比使用矩阵方便的多。
的确对于一般交互，用transform默认提供的方法足够了，但是一些其它效果，没有直接方法，这时就需要使用matrix方法了。
列如参考文档里张鑫旭的镜像对称，可以用matrix矩阵方式，可以做图片的镜像对称。（列如有时候拍照，前置摄像头拍出来的照片是反的，如果有需求还原，可以用这个矩阵的方法复原）