第一部分：奇变偶不变（决定函数名）

· “奇”和“偶”：指的是公式中 π/2 的系数 k 是奇数（1, 3, 5…）还是偶数（2, 4, 6…）。

· 例如：π/2 和 3π/2 的系数是奇数；π 和 2π 的系数是偶数。

· “变”与“不变”：指的是函数名是否需要改变。

· 如果k是奇数，函数名就要改变：

· sin ↔ cos

· tan ↔ cot

· 如果k是偶数，函数名就保持不变。

简单来说：当你看到要化简的角是 π/2 的奇数倍加减α时，就把函数名换成它的余函数；如果是偶数倍，函数名就不变。

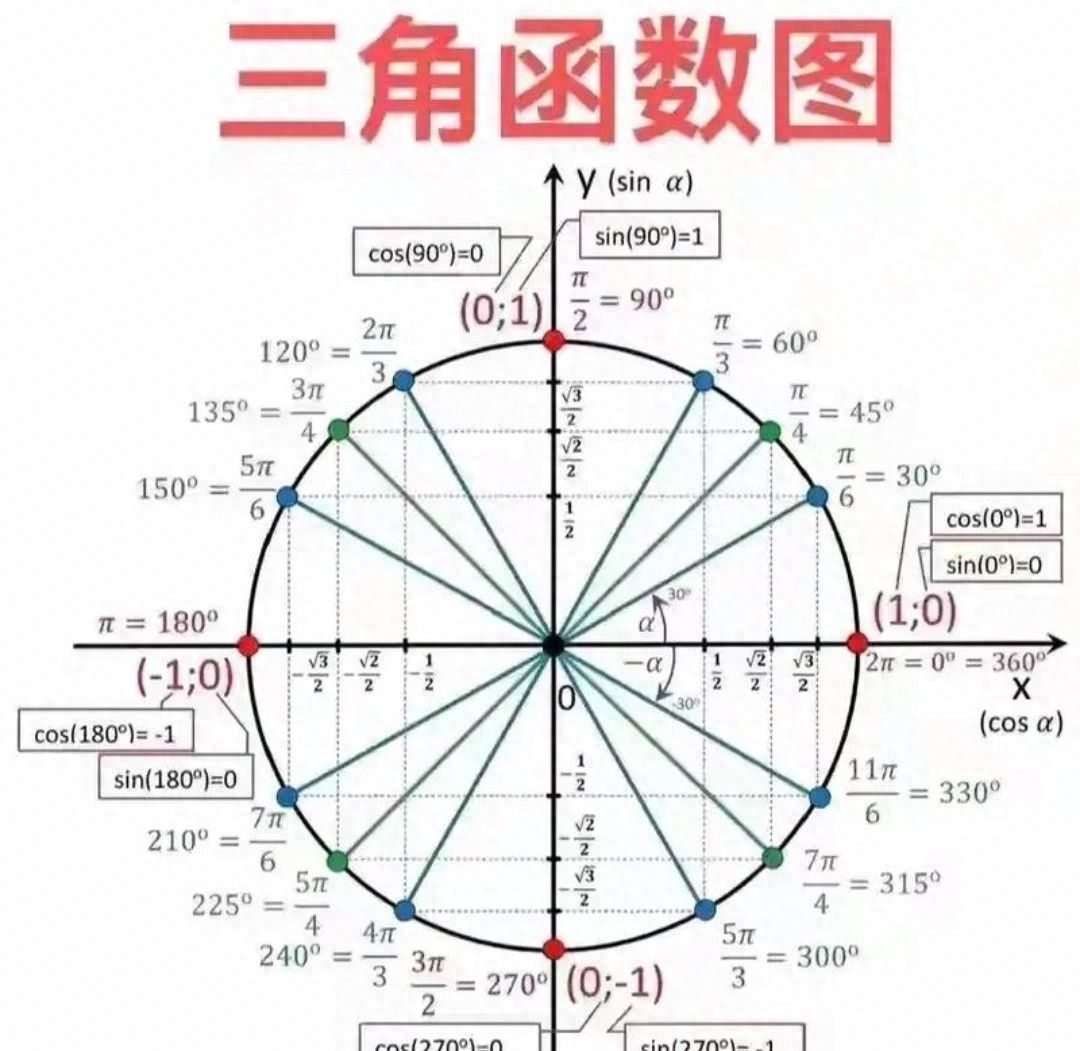
第二部分：符号看象限（决定正负号）

· “符号”：指的是化简后，结果前面的正号（+）或负号（-）。这个符号是口诀的精华，也是最容易出错的地方。

· “看象限”：

1. 关键假设：第一把α假想成一个锐角（即0°到90°之间的角）。

2. 确定原角象限：计算 π/2 * k ± α 这个整体的角有多大，并判断它落在哪个象限。

3. 定号：看原函数（即化简前的函数，如sin、cos等）在你刚刚判断出的那个象限里的符号是什么（是正还是负）。这个符号，就是最终结果前面的符号。

如何记忆象限符号？——ASTC口诀

为了快速知道各象限的符号，请记住“ASTC” 口诀（或“全正，正正弦，正正切，正余弦”）：

· All：第一象限，所有函数都为正。

· Sine：第二象限，只有正弦（sin） 和余割（csc）为正。

· Tangent：第三象限，只有正切（tan） 和余切（cot）为正。

· Cosine：第四象限，只有余弦（cos） 和正割（sec）为正。

简单来说：假设α是锐角，算出原角在哪儿，然后根据原函数的象限符号来给结果定号。

实战示例

让我们通过几个例子来完整使用这个口诀。

例1：化简 sin(π – α)

1. 奇变偶不变：π – α 即 π/2 * 2 – α，系数 k=2（偶数），所以函数名不变，还是 sin。

2. 符号看象限：

· 假设α是锐角，那么 π – α（180° – α）就在第二象限。

· 在第二象限（S），正弦（sin）的符号是正的。

3. 结论：sin(π – α) = + sinα

例2：化简 cos(π/2 + α)

1. 奇变偶不变：π/2 + α 的系数 k=1（奇数），所以函数名要变，cos 变成 sin。

2. 符号看象限：

· 假设α是锐角，那么 π/2 + α（90° + α）就在第二象限。

· 在第二象限（S），余弦（cos）的符号是负的。（注意，这里看的是原函数cos的符号）

3. 结论：cos(π/2 + α) = – sinα

例3：化简 tan(3π/2 – α)

1. 奇变偶不变：3π/2 – α 即 π/2 * 3 – α，系数 k=3（奇数），所以函数名要变，tan 变成 cot。

2. 符号看象限：

· 假设α是锐角，那么 3π/2 – α（270° – α）就在第三象限。

· 在第三象限（T），正切（tan）的符号是正的。

3. 结论：tan(3π/2 – α) = + cotα

例4：化简 sin(2π – α)

1. 奇变偶不变：2π – α 即 π/2 * 4 – α，系数 k=4（偶数），所以函数名不变，还是 sin。

2. 符号看象限：

· 假设α是锐角，那么 2π – α（360° – α）就在第四象限。

· 在第四象限（C），正弦（sin）的符号是负的。

3. 结论：sin(2π – α) = – sinα

总结

· 两步顺序：先“奇变偶不变”确定函数名，再“符号看象限”确定正负号。顺序不能颠倒。

· 核心前提：始终把α当作一个锐角来处理，这是判断象限的基础。

· 万能性：这个口诀适用于所有基本三角函数（sin, cos, tan, cot）的诱导公式。

· 最佳掌握方式：在理解原理后，找几个例子自己动手推导一遍，远比死记硬背所有公式有效。