大数据探索性分析学习笔记-1

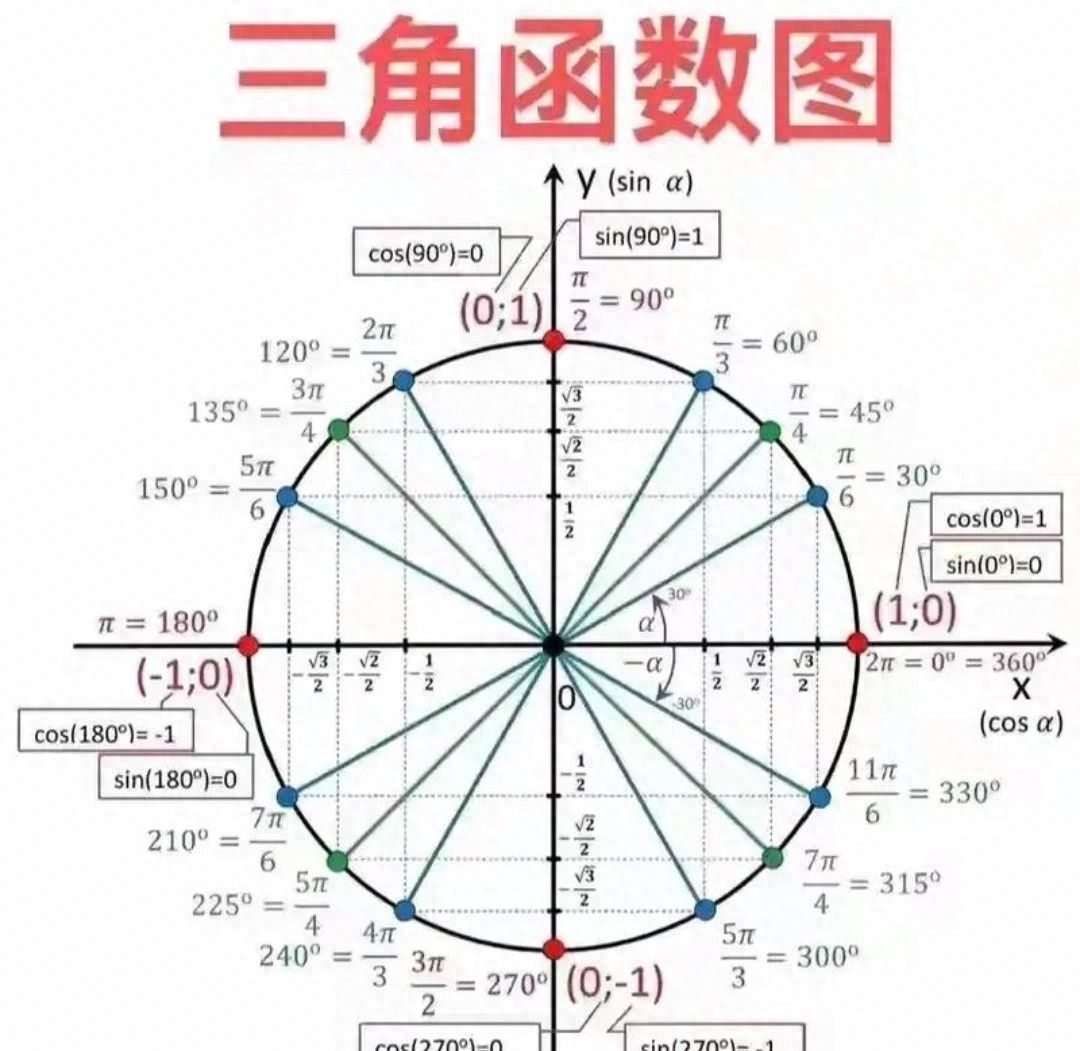
大数据探索性分析基本流程

1）理解数据：了解数据的结构、质量（缺失值、错误值、重复值）、分布（数据取值范围、集中趋势 – 均值/中位数、离散程度 – 方差/标准差）等规律

2）发现线索：识别趋势、异常值、关联

3）形成假设：针对线索，生成可验证的假设

4）检查前提：有很多数据分析模型（如：回归分析，方差分析）都有明确的适用前提，如：正态性（数据分布符合正态分布）、独立性（样本之间无关联）

5）建模准备：包括数据清洗、特征工程（标准化/归一化）

一、数据形式内容

数据的形式（偏概念）

1）结构化数据：以行和列存储，具有固定格式和明确字段含义的数据（便于计算机直接读取的数据）

核心分析方法：SQL查询、回归分析（线性回归预测连续型变量；逻辑回归预测分类型变量）

2）非结构化数据：无固定格式的数据，需要通过半结构化处理才能被分析的数据

核心分析方法：自然语言处理、计算机视觉、语音识别

数据元素的类型：数值型、字符型、布尔值、日期时间型、列表型、字典型

属性的类型：类别型、序数型、区间型、比率型

数据点的相似性度量

纯数值型属性情况：

纯类别型属性情况：

纯序数型属性情况：

混合型属性情况：

案例：

解答：

目标：比较A与B像不像

step 1：计算每个属性的局部距离（不像程度）

1）年龄（数值属性）

局部距离 = A(35)与B(28)年龄差 / 年龄最大范围差  （这里年龄最大范围假设为18 – 70，差为52) = 0.135

2）性别（二元属性）

二人不同性别，局部距离 = 1

3）教育程度（序数属性）

把学历按 “高中 = 1、学士 = 2、硕士 = 3、博士 = 4” 排顺序

局部距离 = A(3)与B(2)的差 / 学历最大范围差(4-1=3) = 0.333

4）购买类别（类别属性）

由于二者完全没有重叠部分，采用Jaccard方法计算

局部距离 = 1-(重叠数/总类别数) = 1

总结一下这部分：

step 2：设置权重，计算加权距离（加权距离为：对应属性权重 * 对应局部距离）

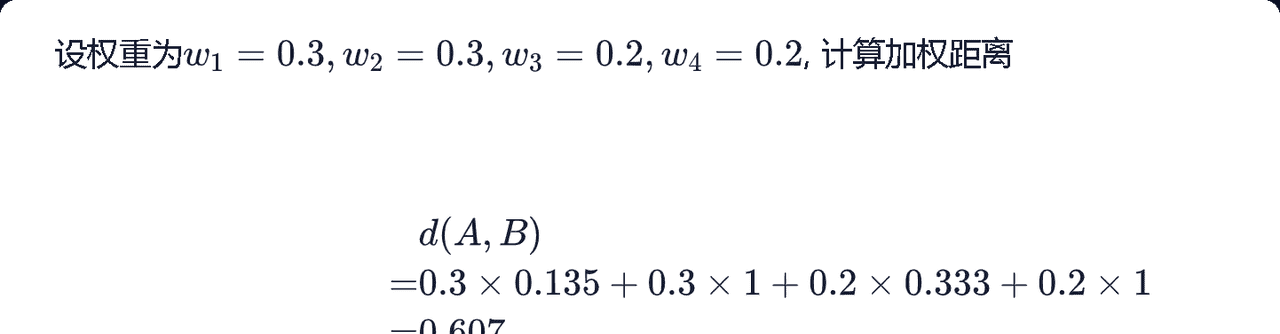
—— 0表示完全相同，1表示完全不同。

二、描述型统计

集中趋势概念：均值、中位数、众数

离散程度：

1）标准差

2）变异系数：消除测量尺度和量纲的影响

如：身高用厘米、体重用公斤，单位不一样没法直接比波动？这时候用变异系数：把标准差除以平均值，去掉单位影响。

3）极差：最大数-最小数

4）四分位差：先把数据排好队，分成 4 等份，取中间那一半的范围（第 3 份减第 1 份）。不管两头的极端值，只看中间大多数数据的波动。

分布形态：偏度、峰度

1）偏度（衡量数据偏移程度）- 偏不偏？

2）峰度（衡量数据集中趋势的指标）- 尖不尖？

偏度是绝对指标、峰度是相对指标

Q1：如何计算样本偏度和峰度？

1）计算样本偏度

样本偏度公式：

2）计算样本峰度

Q2：方差、偏度、峰度的联系？

都是描述数据分布特征的指标

三、属性类型与统计方法的适配

1）类别型属性

核心统计方法：
– 频数：某类别的出现次数
– 频率：某类别出现次数占总数的比例图表：柱状图、饼图

2）序数型属性（数据有顺序/等级，但没有固定的数值间隔）

核心统计方法：
– 累积频数：从低到高（或高到低）累加的次数（比如 “优 + 良” 的累积频数 = 优的频数 + 良的频数）
– 等级相关分析：看两个序数数据的 “顺序关联”（比如 “成绩等级” 和 “作业完成等级” 是否正相关）

图表：折线图、箱线图

3）区间型属性

核心统计方法：均值、方差图表：直方图、散点图

4）比率型属性

核心统计方法：均值、标准差、相关系数（看两个比率数据的 “线性关联强度”（比如 “身高” 和 “体重” 的相关程度））图表：折线图、散点图

四、缺失值

1）缺失值的分类：

完全随机缺失：缺失与任何变量无关，仅由随机因素导致随机缺失：缺失与已观测变量相关，但与缺失变量本身无关非随机缺失：缺失与缺失变量本身直接相关

2）缺失数据的处理步骤

识别缺失值——探索缺失值的分布模式——分析导致缺失的原因——处理缺失值

3）缺失值的处理

删除法：行删除&列删除代表性性数据填充：
– 均值填充：适用于服从正态分布的数值型变量
– 中位数填充：适用于存在极端值的偏态分布
– 众数填充：适用于离散型分布变量
– 前向填充/后向填充：适用于时间序列数据（如：今天的数字空了，就用明天的或者昨天的数据填充）预测法填充：
– 回归填充：通过与缺失值有关联的变量建立回归模型，从而预测缺失值
– KNN填充：找k个与缺失值相似情况的值，取他们的均值从而填充缺失值

五、异常值（= 离群点）

1、概念部分

1）异常值的来源

数据来源于不同的类自然变异数据测量和收集误差业务特征

2）异常值的类型

点异常值上下文异常值集体异常值

3）判断异常值需要注意

确定数据对象是单一属性异常还是多个属性异常异常值的全局观点和局部观点（数据是否异常需要考虑其所对比对象）数据对象的异常程度多个数据对象同时考虑看有没有异常

2、异常值检测

1）基于统计方法检测异常值

a、基于z-score的异常值检测

适用于：单变量+正态分布

z的值 = （当前值 – 均值）/ 标准差

b、基于箱线图的检测

箱线图（= 盒须图）：由中位数Q2、下四分位数Q1、上四分位数Q3构成的箱体以及两个表示数据范围的须线组成，超出上下边缘的值为异常值。

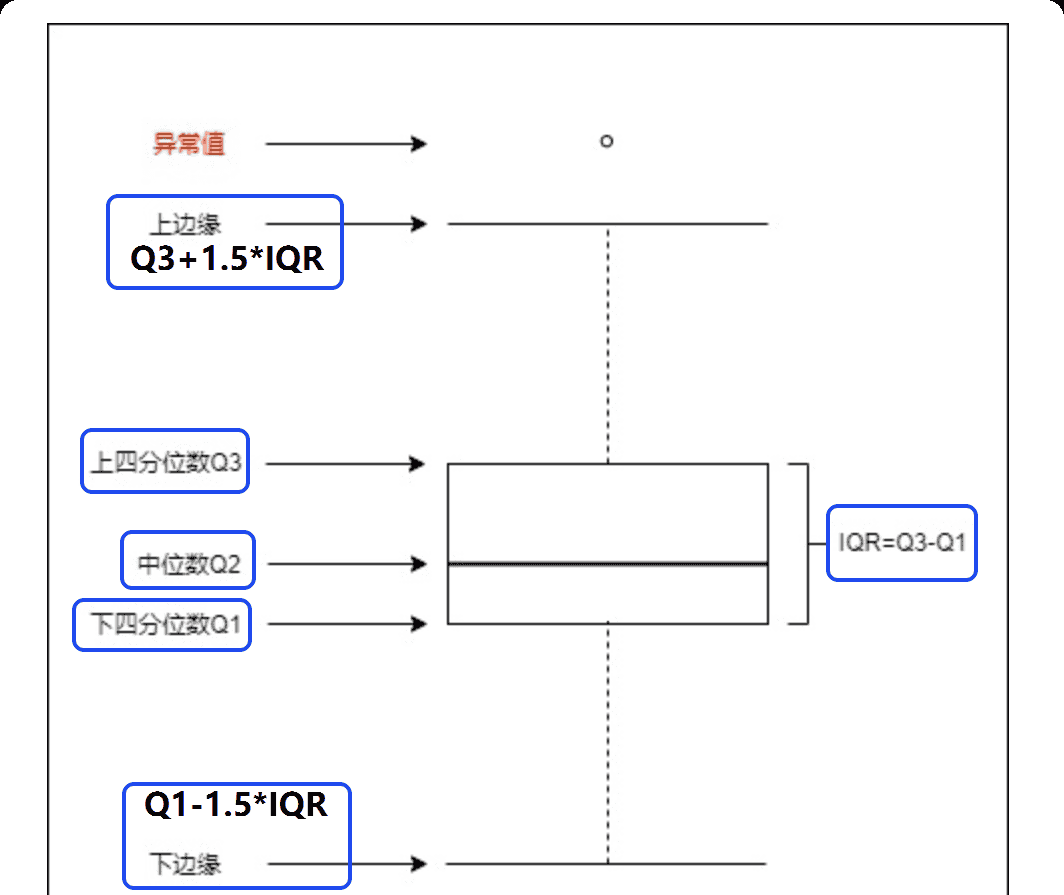
c、基于假设检验的检测

（适合数据少+只有一个异常值点+正态分布的情况）——（可以支持多变量）

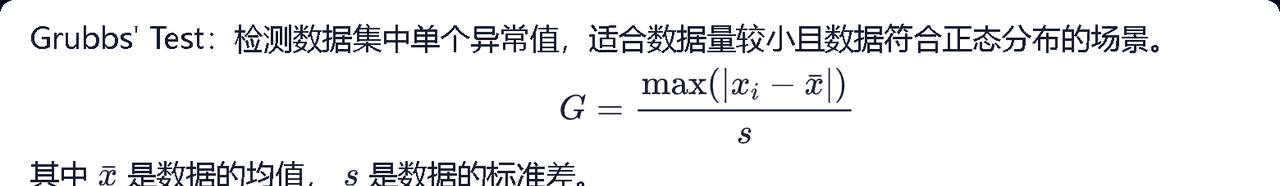
用算出来的G，查表检验（G是否>临界点）该值是否显著，若显著（>），则该点为异常值点。

2）基于局部离群因子检测异常值

局部离群因子（LOF）

定义：通过评估数据对象相对于其局部邻近区域的离群程度来检测异常点，不是通过全局尺度来判定。

异常点位于局部密度较低的区域；正常点位于局部密度较高的区域。

LOF通过比较每个点的局部1密度来判断该点是否为异常点。

计算局部离群因子（LOF）

step1：

对数据集中每个点选取k个离他最近的点

step2：

计算k – 距离（k – distance）= 每个数据点p到与他的第k个最近点ok之间的距离

ok又被称为点p的第k个最近邻

如：第五个点离该点2米，则k – 距离就为2米

step3：

定义可达距离（平滑点之间的距离，避免由于局部过于密集的区域导致的异常点识别误差）

当前点为p

可达距离 = max（o点的k – 距离，p到o之间的距离）

简单来讲：可达距离 = max (邻居的 k – 距离，点到邻居的实际距离)

step4：

局部可达密度（LRD）：邻居到该点的平均可达距离的倒数（密度越高，值越大）

step5：

计算局部离群因子（LOF）

LOF接近于1——为正常点

LOF>1——为异常点

LOF值越大，离群程度越高

k值的影响：k太小，局部信息不够，容易误判；k值越大，异常点会被漏掉

3）基于聚类检测异常值（k – means聚类）

k – means聚类定义：

把所有数据点分为k个簇（k个小团体），计算每个点到自己所属簇的中心的距离，根据这一距离设定阈值，大于这一阈值的被称为离群点。

阈值选择：

k – means聚类的优缺点：

3）基于聚类检测异常值（DBSCAN聚类）

DBSCAN聚类定义：

两个重要参数：最小邻居数（MinPts）；半径参数（eps）

对每个数据点，DBSCAN通过检查它在半径（eps）范围内的邻居数是否达到最小邻居数（>=MinPts）来判断这一数据点是否为核心点。

>=MinPts 则为核心点；<MinPts则为噪声点。

优缺点：

3、异常值的处理

直接删除异常值替换：均值替换；中位数替换；截断（超过异常值边界的值用边界值代替）异常值修正：对数变化（减少右偏分布的影响）；平方根变换（适用于轻微偏移的数据）；Box-Cox变换（通过参数调整数据分布，使其更接近正态分布）分离异常值单独分析

异常值处理的影响评估：

可视化图表（直方图；QQ图——验证正态性）统计量量化（均值，方差，偏度的变化）模型性能的前后验证：如线性回归模型的R2变化；k – means聚类的轮廓系数变化