AI学习笔记系列 – 机器学习（ML）

机器学习

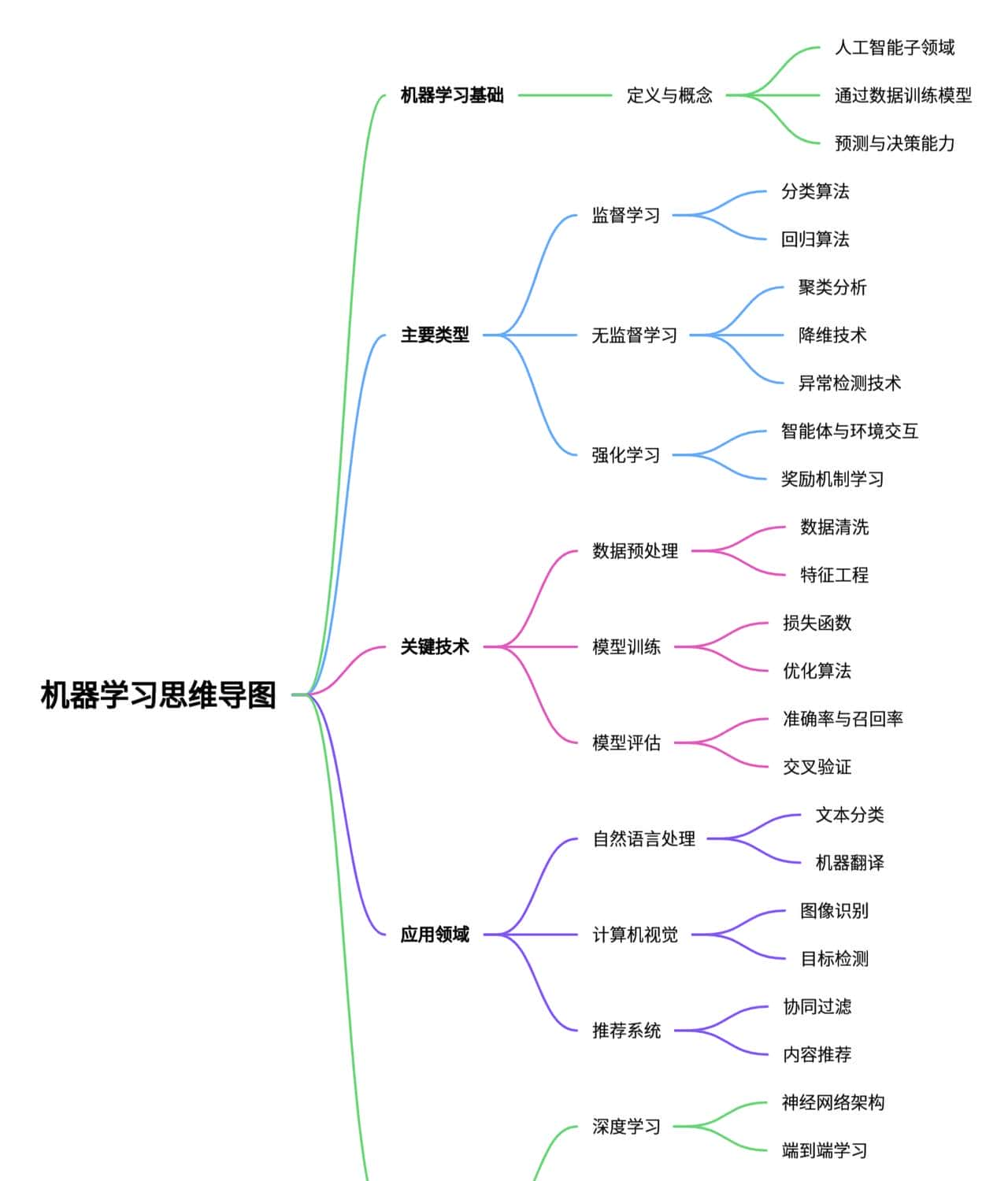
1. 思维导图

2. 简介

2.1 什么是机器学习?

非正式定义：平常我们用的内容搜索（谷歌、百度）、广告推荐、语音识别（Siri）、自动驾驶等都用到了机器学习算法，目前在社会上的各个行业都在尝试使用机器学习解决企业问题， 比如金融、工业，这些通过学习算法预测结果的方法叫做机器学习。正式定义：Field of study that gives computers the ability to learn without being explicitly programmed – Arthur Samuel(1959). Arthur 将机器学习定义为一门研究使计算机能够在不被明确编程的情况下进行学习的学科。（Arthur 设计的跳棋游戏经过数以万计的对弈， 学会了如何更好的玩跳棋，成为了高手， 如果没有数以万计的对弈，它就不会成为高手。

2.2 机器学习分类

机器学习主要类型目前被分为3大类，分别为监督学习、非监督学习和强化学习，给类型定义如下：

监督学习（Supervised Learning）：Learns from being given “right anwsers”. 学习从输入到输出或者说从X映射到Y， 通过大量数据训练， 预测未知输入变量的结果。该类主要包含了常用的回归算法和分类算法。

非监督学习（Unsupervised Learning）：Data only have input X, but not have output labels Y, algorithm has to find the “struture” in the data. 训练数据只有输入变量， 没有给定的输入变量对应的结果，需要学习模型算法把数据按照一定的条件聚类，变成结构化数据，当输入某个未知变量时，模型算法可以给出预测结果。非监督学习主要包含聚类算法、异常检测技术和降维算法。

强化学习（Reinforcing Learning）：待学习

3. 监督学习

3.1 回归算法

3.1.1 线性回归函数

线性回归模型：
常用术语： 
Training set: 训练集
符号：
    x : 输入变量、特征
    y : 输出变量、目标变量
    m : 训练集数量
    (x, y) : 单个训练数据
    (, ): 第i个训练数据

单线性回归模型： f(x) = wx+b
    w, b ： 模型的参数（也称可调参数），是可调整已优化模型的变量

以下使用python 代码实现线性回归计算模型：

#导入 numpy 和 matplotlib 类库
import numpy as np
import matplotlib.pyplot as plt
 
# 定义训练数据集，x表示输入、y表示针对于x的结果
x_train = np.array([1.0,2.0, 3.0,4.0,5.0,6.0,7.0])
y_train = np.array([300,500,600,650,1000,1350,1500])
 
 
# 定义训练集的数据量
m= len(x_train)
print(f"The number of the training set is: {m}")
 
# 定义每一次训练的输入变量， 从第一条数据开始i=0
i=0
x_i = x_train[i]
y_i = y_train[i]
print(f"x^({i}), y^({i}) = ({x_i},{y_i})")
 
# 调用matplotlib.pyplot 库里的scatter函数， 根据训练集数据绘制散点图
plt.scatter(x_train, y_train, marker = 'x', c='r')
plt.title('Houseing Price')
plt.ylabel('Price')
plt.xlabel('Size')
plt.show()
 
# 定义线性回归函数的变量斜率w和常数b
w = 200
b = 100
print(f'w: {w}')
print(f'b: {b}')
 
# 定义线性回归函数计算模型f(x) = wx + b, 根据输入参数w、b、x返回函数执行结果值
def calculation_model_output(w,b,x):
    m = x.shape
    f_wb = np.zeros(m)
    for i in range(len(x)):
        f_wb[i] = w * x[i] + b
 
    return f_wb
 
# 调用 pyplot 库中的plot方法，绘制线性回归函数，调用scatter 绘制最终线性函数图
temp_f_wb = calculation_model_output(w, b, x_train)
plt.plot(x_train, temp_f_wb, c='b', label='Our Prediction')
plt.scatter(x_train, y_train, marker = 'x', c='r', label = 'Actual Value')
plt.title('Housing Price')
plt.ylabel('Price')
plt.xlabel('Size')
plt.legend()
plt.show()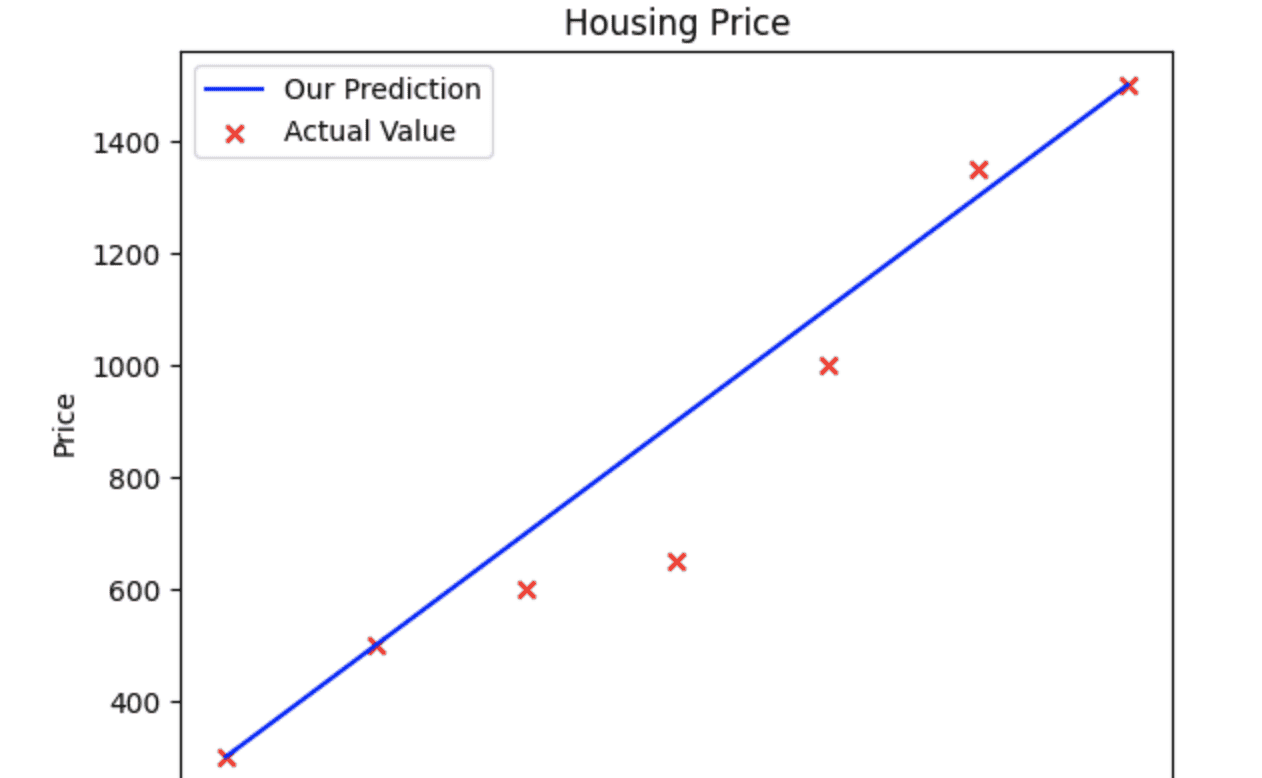

以上就是线性回归函数 f(x) = wx + b 的模型， 可以看出，函数的结果准不准取决于参数w和b的定义，如何找到只合适的w和b 的值，是线性回归模型的重要事情，在数学领域， 我们一般使用方差来判断数据的离散程度，所以假设我们根据此模型预测出来的房价是y^(i), 根据线性回归模型函数计算出来的房价是y(i), 那么y^(i) 和y(i) 的离散程度越小，则表明房价预测越准确， 由此引出了成本函数的概念。

3.1.2 成本函数

 : 表示成本函数的值

: 表示线性回归函数得到的预测值

: 表示线性回归函数得到的实际值

以下使用python 代码实现成本函数计算模型：

import numpy as np
import matplotlib.pyplot as plt
 
def compute_cost(X, y, theta):
    """
    计算线性回归的成本函数（均方误差）
    
    参数:
    X -- 特征矩阵，形状为(m, n)，m为样本数，n为特征数（包括偏置项）
    y -- 真实值向量，形状为(m,)
    theta -- 参数向量，形状为(n,)
    
    返回:
    cost -- 计算出的成本值
    """
    m = len(y)  # 样本数量
    predictions = X.dot(theta)  # 模型预测值：X * theta
    errors = predictions - y  # 预测误差
    cost = (1 / (2 * m)) * np.sum(errors ** 2)  # 均方误差成本函数
    return cost
 
# 1. 准备示例数据（房屋面积与价格）
# 假设我们有一些数据点
np.random.seed(42)  # 确保结果可重现
m = 50  # 样本数量
X_raw = 2.5 * np.random.randn(m) + 1.5  # 房屋面积特征
residuals = 1.2 * np.random.randn(m)
y = 2 + 0.3 * X_raw + residuals  # 房屋价格（目标值）
 
# 为特征矩阵X添加一列1，用于theta_0（截距项）
X = np.c_[np.ones(m), X_raw]
 
# 2. 计算不同参数下的成本（为绘图做准备）
# 生成一组theta值进行测试
theta0_vals = np.linspace(-1, 5, 100)  # theta0的可能取值
theta1_vals = np.linspace(-0.5, 1.5, 100)  # theta1的可能取值
 
# 初始化一个矩阵来存储成本值
J_vals = np.zeros((len(theta0_vals), len(theta1_vals)))
 
# 计算每个(theta0, theta1)组合对应的成本
for i, t0 in enumerate(theta0_vals):
    for j, t1 in enumerate(theta1_vals):
        theta_test = np.array([t0, t1])
        J_vals[i, j] = compute_cost(X, y, theta_test)
 
# 3. 绘制成本函数图
# 创建图形和子图布局
fig = plt.figure(figsize=(16, 6))
 
# 子图1：3D曲面图
ax1 = fig.add_subplot(121, projection='3d')
T0, T1 = np.meshgrid(theta0_vals, theta1_vals)  # 创建网格
surf = ax1.plot_surface(T0, T1, J_vals.T, cmap='viridis', alpha=0.8)  # 绘制曲面
ax1.set_xlabel('b', fontsize=12)
ax1.set_ylabel('w', fontsize=12)
ax1.set_zlabel('J(w,b)', fontsize=12)
ax1.set_title('Cost Function 3D', fontsize=14)
fig.colorbar(surf, ax=ax1, shrink=0.5, aspect=5)  # 添加颜色条
 
# 子图2：等高线图
ax2 = fig.add_subplot(122)
contour_levels = np.logspace(-1, 3, 20)  # 定义等高线层级（使用对数刻度）
contour = ax2.contour(T0, T1, J_vals.T, levels=contour_levels, cmap='viridis')  # 绘制等高线
ax2.set_xlabel('b', fontsize=12)
ax2.set_ylabel('w', fontsize=12)
ax2.set_title('Cost Function Contour Map', fontsize=14)
plt.colorbar(contour, ax=ax2)  # 添加颜色条
 
# 标记成本最低的点（大致的最优解）
min_idx = np.unravel_index(np.argmin(J_vals), J_vals.shape)  # 找到最小成本的索引
min_theta0 = theta0_vals[min_idx[0]]
min_theta1 = theta1_vals[min_idx[1]]
ax2.plot(min_theta0, min_theta1, 'rx', markersize=10, markeredgewidth=2, label='min-cost-point')
ax2.legend()
 
plt.tight_layout()  # 自动调整子图参数，使之填充整个图像区域
plt.show()
 
# 输出最优参数和最小成本值
min_cost = np.min(J_vals)
print(f"近似最优参数: theta0 = {min_theta0:.2f}, theta1 = {min_theta1:.2f}")
print(f"最小成本值: {min_cost:.4f}")

执行代码获得如下结果：

左图中的谷底表明在训练的数据集中，的值最小，在右图的等高线图中的表现为中心x的值对应的w和b 是本次训练集中最理想的取值。有了的最小值， 在算法的实现中， 我们使用梯度下降算法来获取w和b的值。

3.1.3 梯度下降算法

以下是梯度下降算法中w和b的值的公式，其中是学习率， 是一个介于(0,1)中间的一个值， 表示梯度下降的步长。表示对w的偏导数，表示对b的偏导数。

根据成本函数的定义， 我们可以将上面w的公式偏导计算转换为以下的计算公式：

同理可得出b 的偏导公式：

下面用python实现梯度下降算法：