回归模型评估的全面介绍

介绍

机器学习模型旨在理解数据中的模式，从而实现预测、回答问题或更深入地理解隐藏的模式。这个迭代学习过程涉及模型获取模式、针对新数据进行测试、调整参数，并重复直到达到令人满意的性能。评估阶段对于回归问题至关重大，使用损失函数。作为数据科学家，监控 回归指标 如均方误差和R平方，以确保模型不会过拟合训练数据，这一点至关重大。像 scikit-learn 这样的库提供了训练和评估回归模型的工具，协助数据科学家构建有效的解决方案。

学习目标:

• 了解损失函数在评估回归模型中的作用。
• 了解不同类型的回归损失函数及其应用。
• 确定各种回归评估指标的优缺点。
• 获得使用Python库实施回归指标的实践经验。
• 培养根据特定数据特征和建模需求选择合适损失函数的能力。

目录

0. 介绍
1. 损失函数在模型评估中的作用
2. 选择损失函数的关键因素
3. List of Top 13 Evaluation Metrics
4. 平均绝对误差 (MAE)
5. 平均偏差误差 (MBE)
6. 相对绝对误差 (RAE)
7. 平均绝对百分比误差 (MAPE)
8. 均方误差 (MSE)
9. 均方根误差 (RMSE)
10. 相对平方误差 (RSE)
11. 归一化均方根误差 (NRMSE)
12. 相对均方根误差 (RRMSE)
13. 均方根对数误差 (RMSLE)
14. Huber 损失
15. 对数双曲余弦损失
16. 分位数损失
17. 结论

损失函数在模型评估中的作用

损失函数比较模型的预测值与实际值，评估其在映射X（特征）与Y（目标）之间关系的有效性。损失表明预测值与实际值之间的差异，指导模型的改善。更高的损失表明性能较差，需进行调整以实现最佳训练。

选择损失函数的关键因素

选择合适的损失函数取决于各种因素，如算法、数据异常值和对可微性的需求。可选择的选项众多，每种函数都有其独特的属性，因此不存在通用的解决方案。本文全面列出了回归损失函数，概述了它们的优点和缺点。代码示例可以在不同的库中实现，使用NumPy来增强底层机制的透明度。

让我们毫不延迟地深入回归损失函数的世界。

前13个评估指标列表

这里是13个评估指标的列表。

• 平均绝对误差 (MAE)
• 平均偏差误差 (MBE)
• 相对绝对误差 (RAE)
• 平均绝对百分比误差 (MAPE)
• 均方误差 (MSE)
• 均方根误差 (RMSE)
• 相对平方误差 (RSE)
• 标准化均方根误差 (NRMSE)
• 相对均方根误差 (RRMSE)
• 均方根对数误差 (RMSLE)
• Hyber 损失
• 对数余弦损失
• 分位数损失

平均绝对误差 (MAE)

平均绝对误差，或L1损失，是最简单和易于理解的损失函数和评估指标之一。它是通过计算数据聚焦预测值与实际值之间的绝对差的平均值来得出的。在数学上，它表明绝对误差的算术平均值，专注于其大小，而不思考方向。较低的MAE表明模型的准确性更高。

MAE 公式为：

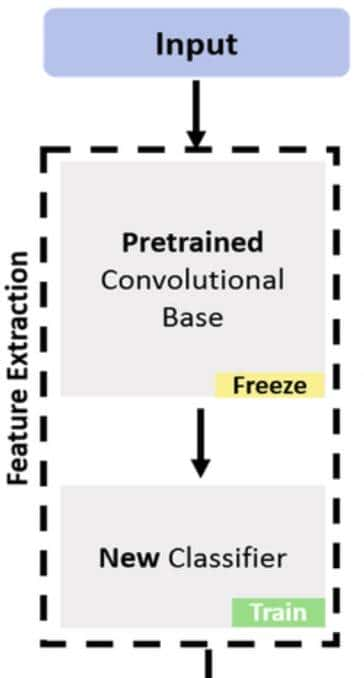
其中

• y_i = 实际值
• y_hat_i = 预测值
• n = 样本大小

Python 代码:

import numpy as np

def mean_absolute_error(true, pred):

    """

    计算真实值与预测值之间的平均绝对误差（MAE）。

        参数：

            true (numpy.ndarray): 真实值的数组。

            pred (numpy.ndarray): 预测值的数组。

        返回：

            float: 平均绝对误差。

    """

    mae = np.mean(np.abs(true - pred))

    return mae

MAE评估指标的优点

• 这是一个易于计算的评估指标。
• 所有的错误都按一样的标准加权，由于思考了绝对值。
• 如果训练数据中有异常值，这很有用，由于MAE不会惩罚由异常值导致的高误差。
• 它提供了一个均衡的指标来评估模型的表现。

MAE评估指标的缺点

• 有时候，来自离群点的大误差最终被视为与低误差一样。
• MAE遵循一种尺度依赖的精度度量，使用与被测数据一样的尺度。因此，它不能用于比较使用不同度量的系列。
• MAE的主要缺点之一是其在零点不可导。许多优化算法倾向于使用微分来寻找评估指标中参数的最优值。
• 在MAE中计算梯度可能会很困难。

平均偏差误差 (MBE)

在“均值偏差误差”中，偏差反映了测量过程高估或低估参数的倾向。它有一个单一方向，正向或负向。正偏差意味着高估的误差，而负偏差则意味着低估的误差。均值偏差误差（MBE）计算预测值与实际值之间的平均差异，量化整体偏差而不思考绝对值。与平均绝对误差（MAE）类似，MBE的不同之处在于不取绝对值。使用MBE时需要谨慎，由于正误差和负误差可能会相互抵消。

MBE的公式：

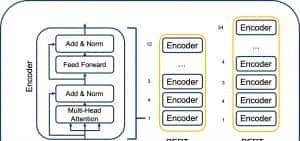
    def mean_bias_error(true, pred):
    bias_error = true - pred
    mbe_loss = np.mean(np.sum(diff) / true.size)  # 计算均值偏差损失
    return mbe_loss

MBE评估指标的优点

• MBE是一种良好的度量，如果你想检查模型的方向（即是否存在积极或消极的偏差）并纠正模型偏差。

MBE评估指标的缺点

• 这在量级上不是一个好的衡量标准，由于误差往往会相互抵消。
• 它不是超级可靠，由于有时高个体误差会产生低的MBE。
• 作为评估指标，它在一个方向上可能始终不正确。例如，如果你尝试预测交通模式，它始终显示的交通量低于实际观察到的数量。

相对绝对误差 (RAE)

相对均方根误差绝对误差是通过将总绝对误差除以均值与实际值之间的绝对差来计算的。RAE的公式为：

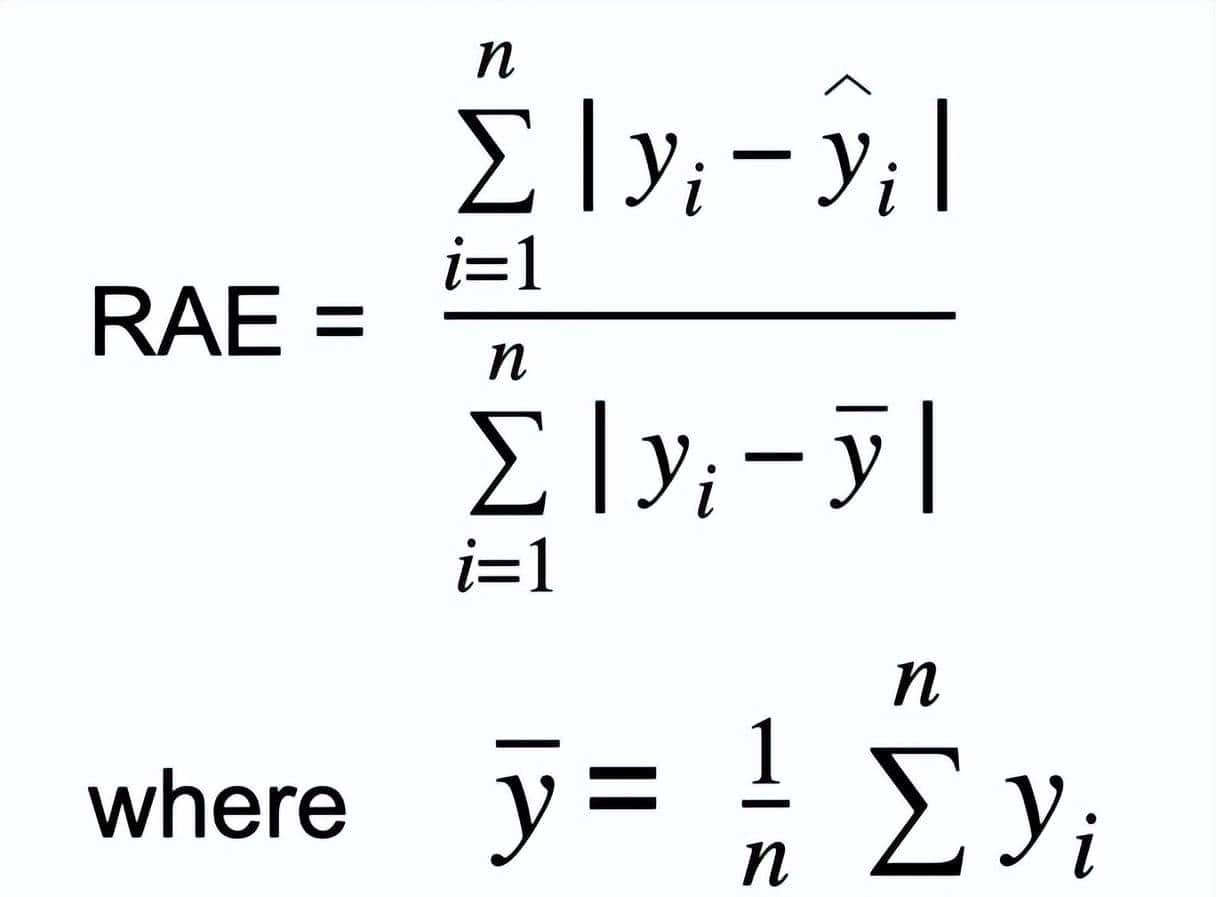
其中 y_bar 是 n 个实际值的均值。

RAE 衡量预测模型的性能，并以比例的形式表明。RAE 的值可以从零到一。一个好的模型将具有接近零的值，而零是最佳值。这个误差显示了均方残差与目标函数的均值偏差之间的关系。

    def relative_absolute_error(true, pred):
    true_mean = np.mean(true)
    squared_error_num = np.sum(np.abs(true - pred))
    squared_error_den = np.sum(np.abs(true - true_mean))
    rae_loss = squared_error_num / squared_error_den
    return rae_loss

RAE评估指标的优点

• RAE 可以用于比较误差以不同单位测量的模型。
• 在某些情况下，RAE 是可靠的，由于它提供了对离群值的保护。

RAE评估指标的缺点

• RAE的一个主要缺点是，当参考预测等于真实值时，它可能是未定义的。

平均绝对百分比误差 (MAPE)

计算平均绝对百分比误差（MAPE），方法是将实际值与预测值之间的绝对差值除以实际值。这个绝对百分比在整个数据聚焦取平均。MAPE，也称为平均绝对百分比偏差（MAPD），随着误差线性增加。较低的MAPE值表明更好的模型性能。

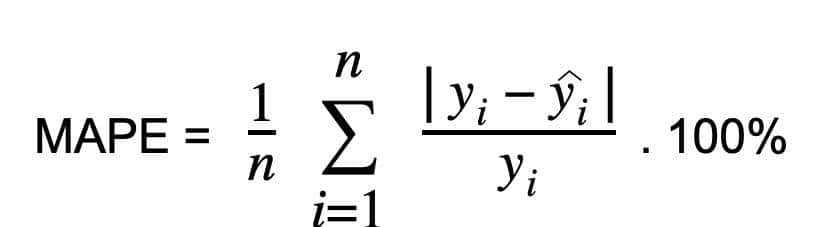
    def mean_absolute_percentage_error(true, pred):
    abs_error = (np.abs(true - pred)) / true
    sum_abs_error = np.sum(abs_error)
    mape_loss = (sum_abs_error / true.size) * 100
    return mape_loss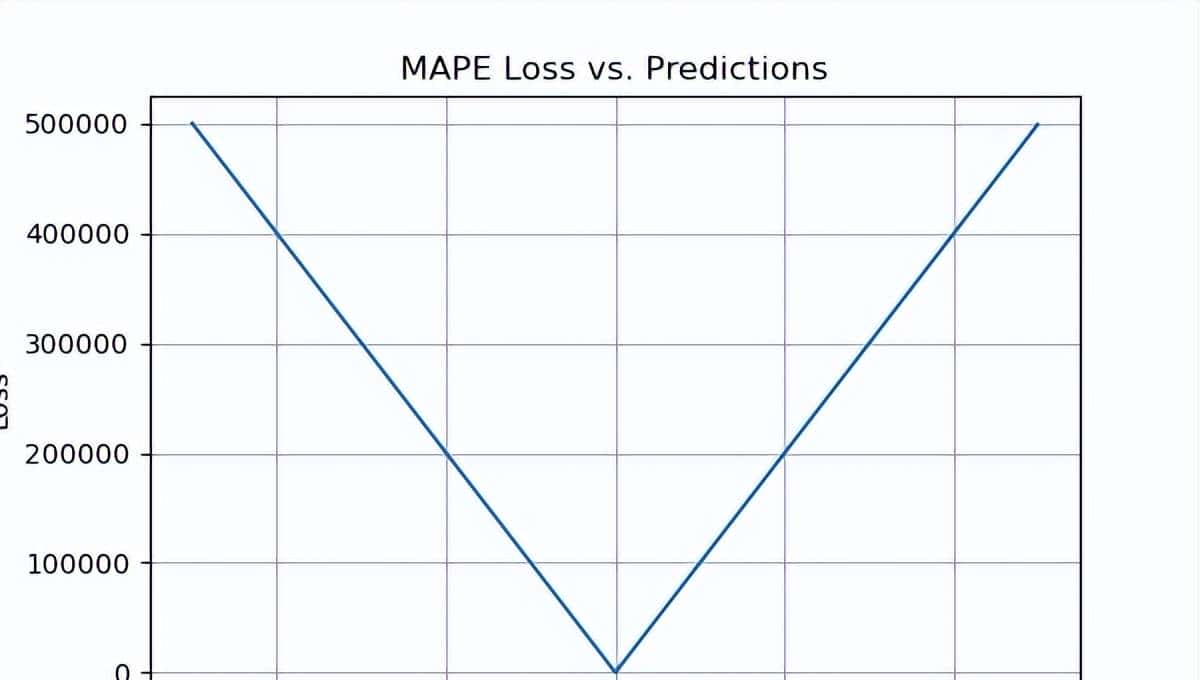

MAPE评估指标的优点

• MAPE是独立于变量的规模，由于它的误差估计以百分比的形式表明。
• 所有错误都归一化到一个共同的标准上，易于理解。
• 由于 MAPE 使用绝对百分比误差，避免了正值和负值相互抵消的问题。

MAPE评估指标的缺点

• MAPE在分母为零时面临一个关键问题，导致“除零”挑战。
• MAPE 通过对负误差的惩罚高于正误差，表现出偏倚，可能会偏向具有较低值的方法。
• 由于除法运算，MAPE 对实际值变化的敏感性导致一样错误的损失不同。例如，实际值为 100 和预测值为 75 的情况下，损失为 25%；而实际值为 50 和预测值为 75 的情况下，损失则更高，为 50%，尽管错误都是 25。

均方误差 (MSE)

MSE 是最常见的回归损失函数之一，也是一个重大的误差指标。在均方误差（Mean Squared Error），也称为 L2 损失中，我们通过平方预测值与实际值之间的差异并对整个数据集取平均来计算误差。

MSE 也被称为二次损失，由于惩罚不是与错误成正比，而是与错误的平方成正比。对错误进行平方会对异常值给予更高的权重，这会导致小错误的平滑梯度。

优化算法从这种对大错误的惩罚中受益，由于它有助于使用最小二乘法找到参数的最优值。均方误差（MSE）永远不会是负数，由于误差是平方的。误差的值范围从零到无穷大。随误差增加，均方误差（MSE）呈指数增长。一个好的模型将具有更接近零的均方误差（MSE）值，表明对数据的拟合优度更好。

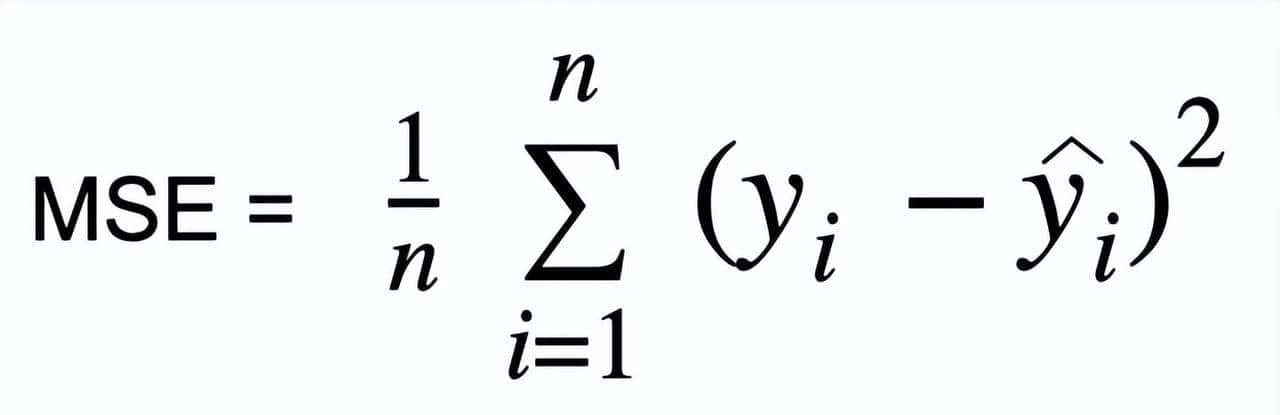
    def mean_squared_error(true, pred):
    squared_error = np.square(true - pred) 
    sum_squared_error = np.sum(squared_error)
    mse_loss = sum_squared_error / true.size
    return mse_loss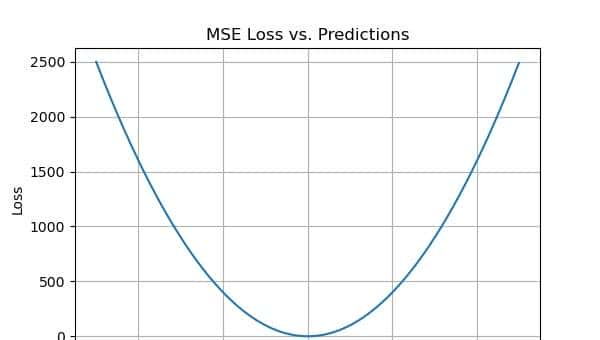

MSE评估指标的优点

• MSE值以二次方程的形式表明。因此，当我们绘制它时，我们得到了一个只有一个全局最小值的梯度下降。
• 对于小错误，它有效地收敛到最小值。没有局部最小值。
• MSE通过对错误进行平方来惩罚模型的巨大错误。
• 它特别有助于通过对具有较大误差的异常值加大权重来剔除模型中的异常值。

MSE评估指标的缺点

• MSE的一个优点在于出现不良预测时变成了缺点。对异常值的敏感性通过对误差进行平方放大了高误差。
• MSE对于单个大错误的影响与太多小错误的影响是一样的。但我们主要还是希望寻找一个在整体表现上足够优秀的模型。
• MSE 是尺度依赖的，由于它的尺度取决于数据的尺度。这使得比较不同的度量超级不可取。
• 当新的异常值被引入数据中时，模型将尝试将该异常值纳入。这样会产生不同的最佳拟合线，这可能导致最终结果出现偏差。

均方根误差 (RMSE)

均方根误差（RMSE）是机器学习和统计中常用的指标，用于衡量预测模型的准确性。它量化了预测值与实际值之间的差异，通过平方误差、取均值，然后开平方来计算。RMSE清晰地说明了模型的性能，较低的值表明相对较好的预测准确性。

它是通过取均方误差（MSE）的平方根来计算的。 RMSE也被称为均方根偏差。它测量误差的平均大小，并关注与实际值的偏差。RMSE值为零表明模型完美拟合。RMSE越低，模型及其预测越好。在机器学习中，相对均方根误差较高表明残差与真实值之间存在较大偏差。RMSE可以与不同特征一起使用，由于它有助于确定特征是否在改善模型预测。

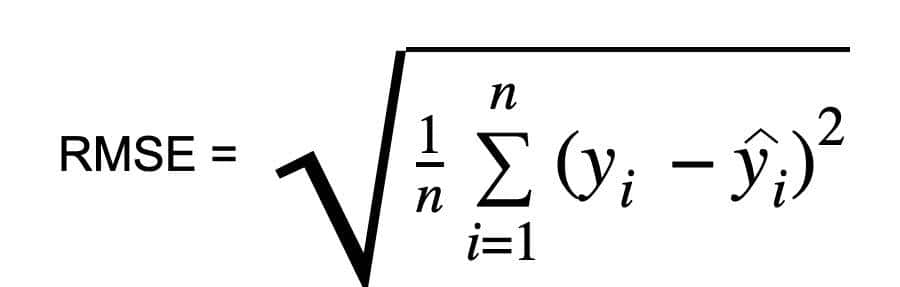
    def root_mean_squared_error(true, pred):
    squared_error = np.square(true - pred) 
    sum_squared_error = np.sum(squared_error)
    rmse_loss = np.sqrt(sum_squared_error / true.size)
    return rmse_loss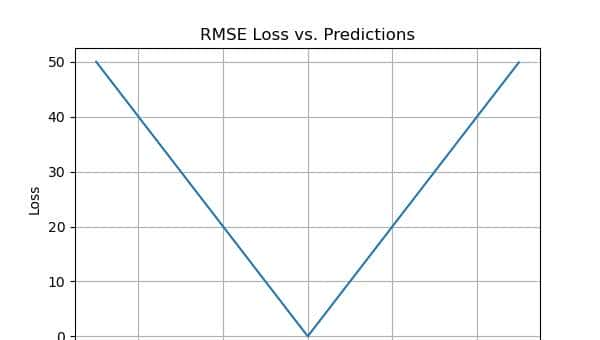

RMSE评估指标的优点

• RMSE 很容易理解。
• 它作为训练模型的启发式方法。
• 它在计算上简单且易于求导，这也是许多优化算法所期望的。
• RMSE由于开方的缘由，对错误的惩罚程度不如MSE那么高。

RMSE指标的缺点

• 像MSE一样，RMSE依赖于数据的规模。如果误差的规模增加，它的数值也会增加。
• RMSE的一个主要缺点是对异常值的敏感性，必须去除异常值才能使其正常工作。
• RMSE 随着测试样本大小的增加而增加。当我们在不同的测试样本上计算结果时，这是一个问题。

相对平方误差 (RSE)

要计算相对平方误差，您需要取均方误差（MSE），并将其除以实际值与数据均值之间差的平方。换句话说，我们将模型的MSE除以使用均值作为预测值的模型的MSE。

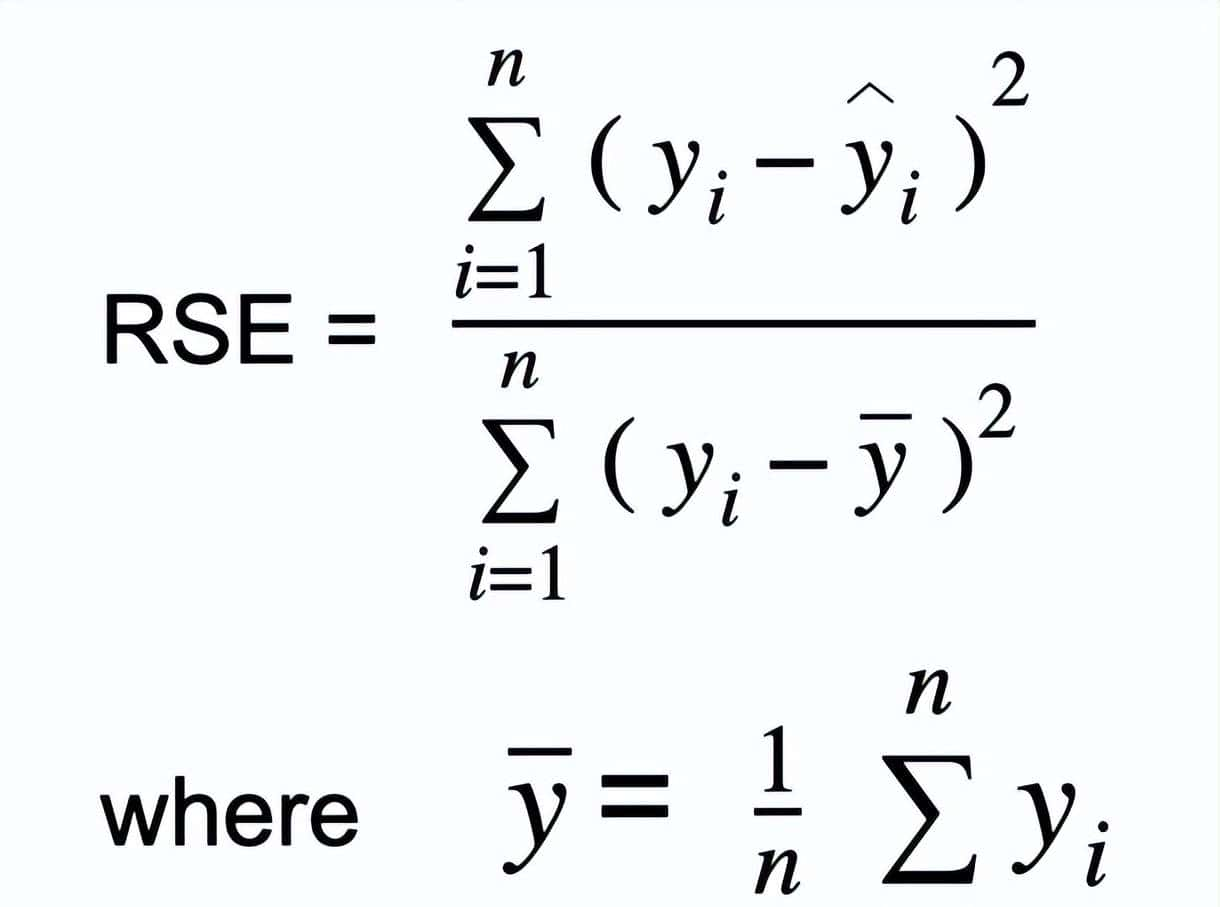
    def relative_squared_error(true, pred):
    true_mean = np.mean(true)
    squared_error_num = np.sum(np.square(true - pred))
    squared_error_den = np.sum(np.square(true - true_mean))
    rse_loss = squared_error_num / squared_error_den
    return rse_loss

RSE的输出值以比率表明。它的范围从零到一。一个好的模型应该有一个接近零的值，而一个值大于1的模型是不合理的。

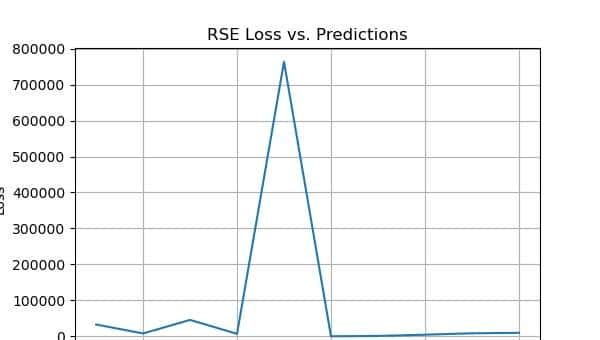
RSE评估指标的优点

• RSE不是尺度依赖的。因此，可以用来比较误差单位不同的模型。
• RSE对预测的均值和尺度不敏感。

RSE评估指标的缺点

• RSE并不区分低估和高估的误差，由于它仅思考y_pred和真实值之间的平方差。这意味着一个始终高估或低估的模型依旧可以具有较低的RSE值。
• 像均方误差（MSE）一样，RSE也受到数据点中离群值的强烈影响。一些极端错误可能会显著增加RSE值，即使模型在大多数数据上表现良好。
• 当RSE值远大于1时，解读性能不佳的程度变得困难。RSE为2或10表明模型的表现比平均预测基线差，但差距的大小并不明确。
• RSE的解释取决于目标值的均值预测基线的表现。如果均值预测本身是一个较差的基线，RSE值可能无法提供有意义的比较。
• 虽然RSE在目标变量单位上是与规模无关的，但它依旧可能对目标值的规模敏感。如果目标变量的范围很小，小误差可能导致大的RSE值，使得该指标信息量降低。
• 对于目标值严格非负的回归分析问题（例如，计数数据或正值），均值预测基线可能不是与自变量进行比较的有意义或合适的基线。
• 对RSE的解释也可能依赖于用于评估的具体测试集。如果测试集不能代表整体数据分布，则RSE值可能无法准确反映模型的性能。

标准化均方根误差 (NRMSE)

标准化RMSE一般通过除以一个标量值来计算。它可以有不同的方式，例如，

• RMSE / 序列中的最大值
• RMSE / 平均值
• RMSE / 最大值与最小值之间的差 (如果均值为零)
• RMSE / 标准差
• 均方根误差 / 四分位范围

# 使用标准差实现NRMSE
def normalized_root_mean_squared_error(true, pred):
    squared_error = np.square((true - pred))
    sum_squared_error = np.sum(squared_error)
    rmse = np.sqrt(sum_squared_error / true.size)
    nrmse_loss = rmse/np.std(pred)
    return nrmse_loss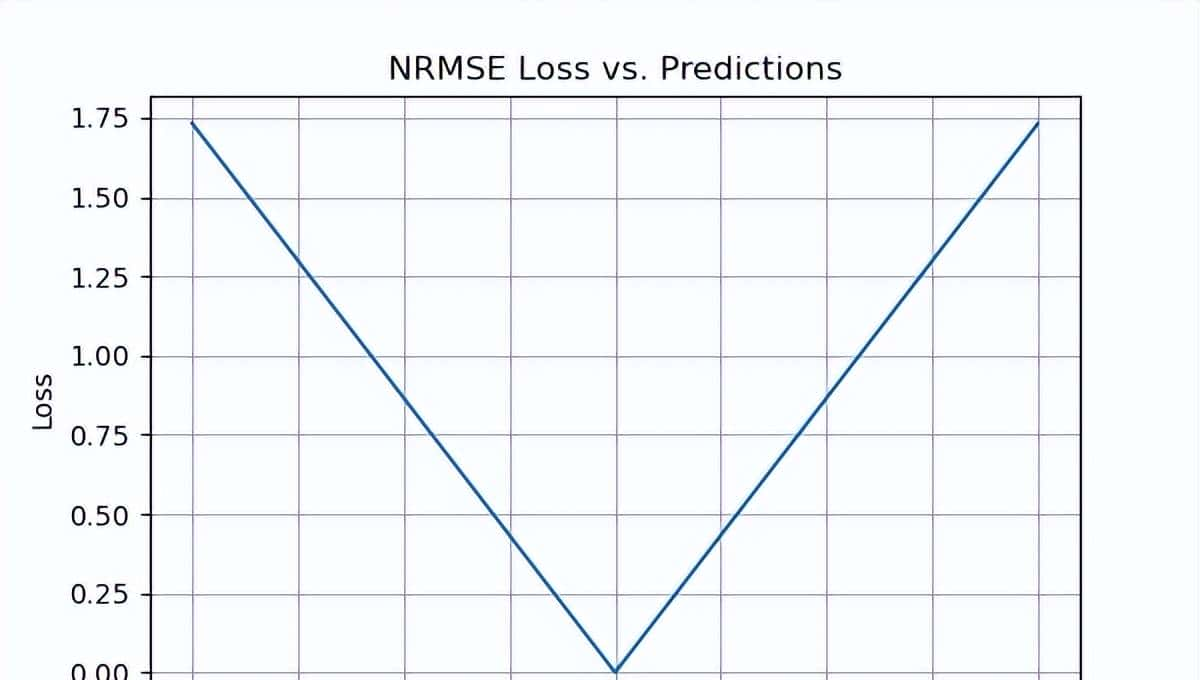

选择四分位数范围可能是最合适的选择，尤其是在处理异常值时。NRMSE对比较具有不同因变量的模型或进行对数变换或标准化等修改时超级有效。该指标解决了尺度依赖性问题，有助于对不同尺度或数据集的模型进行比较。

相对均方根误差 (RRMSE)

相对均方根误差 (RRMSE) 是机器学习中均方根误差 (RMSE) 的一种变体，用于衡量预测模型相对于目标变量范围的准确性。它通过目标变量范围对 RMSE 进行归一化，并将其以百分比形式呈现，以便于跨数据集或跨变量的比较。RRMSE 是 RMSE 的无量纲形式，通过实际值对残差进行缩放，从而允许比较不同的测量技术。

• 当 RRMSE < 10% 时优秀
• RRMSE在10%到20%之间时表现良好
• 当RRMSE在20%到30%之间时，结果是公平的
• 当 RRMSE > 30% 时表现差

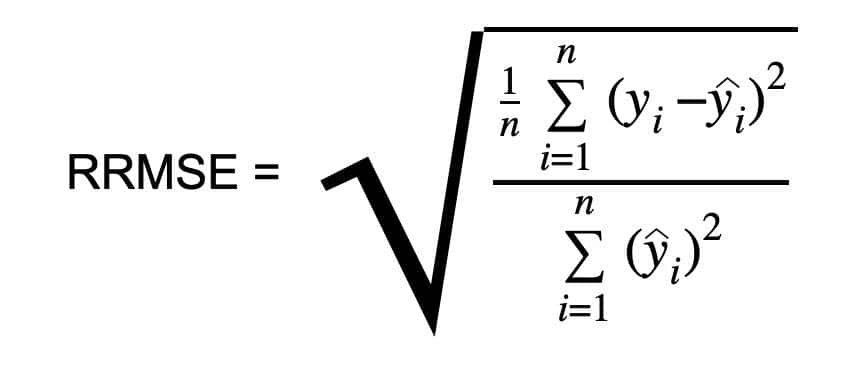
    def relative_root_mean_squared_error(true, pred):
    num = np.sum(np.square(true - pred))
    den = np.sum(np.square(pred))
    squared_error = num/den
    rrmse_loss = np.sqrt(squared_error)
    return rrmse_loss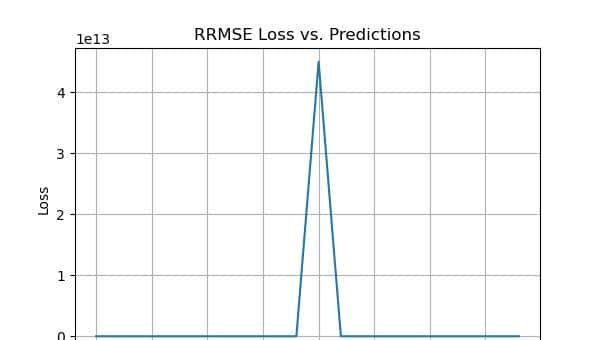

均方根对数误差 (RMSLE)

均方根对数误差是通过对实际值和预测值应用对数，然后计算它们之间的差异来计算的。RMSLE对异常值具有鲁棒性，小误差和大误差被平等对待。

如果预测值低于实际值，则模型会受到更大的惩罚，而如果预测值高于实际值，模型的惩罚就较小。由于对数的存在，它不会惩罚高误差。因此，模型对于低估的惩罚比高估更大。这在我们不在乎高估但低估不可接受的情况下是超级有协助的。

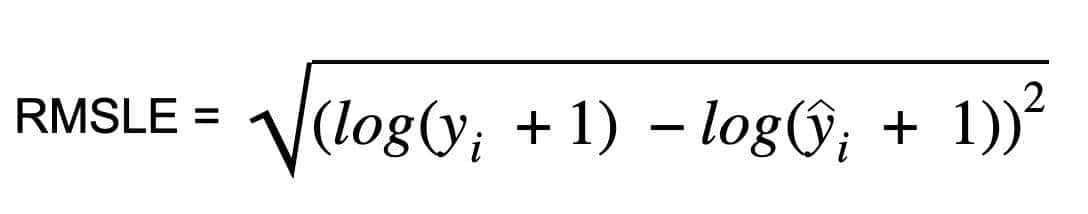
    def root_mean_squared_log_error(true, pred):
    square_error = np.square((np.log(true + 1) - np.log(pred + 1)))
    mean_square_log_error = np.mean(square_error)
    rmsle_loss = np.sqrt(mean_square_log_error)
    return rmsle_loss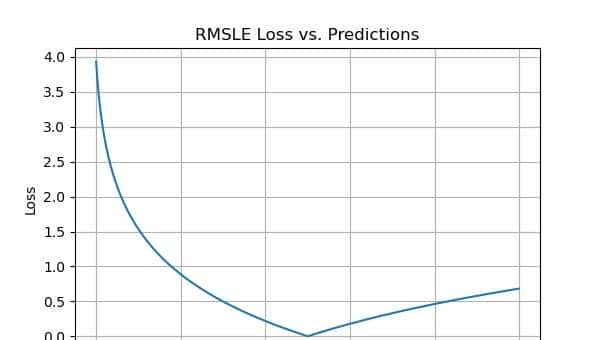

RMSLE评估指标的优点

• RMSLE 不依赖于规模，并且在多种规模下都很有用。
• 它不受大型异常值的影响。
• 它只思考实际值和预测值之间的相对误差。

RMSLE评估指标的缺点

• 它有一个偏向性的惩罚，惩罚低估的程度大于高估。

Huber 损失

如果你想要一个既能学习异常值又能忽略它们的函数怎么办？那么，Huber损失就是为你准备的。Huber损失是线性和二次评分方法的结合。它有一个超参数delta ()，可以根据数据调整。对于超过delta的值，损失将是线性的（L1损失），而对于低于delta的值，则是二次的（L2损失）。它平衡并结合了MAE（平均绝对误差）和MSE（均方误差）的良好特性。

换句话说，对于小于 delta 的损失值，将使用 MSE，而对于大于 delta 的损失值，将使用 MAE。delta () 的选择是极其关键的，由于它定义了我们对离群值的选择。Huber 损失通过使用 MAE 来减少我们对较大损失值的离群值的权重，而对于较小的损失值，则保持使用 MSE 的二次函数。

![huber loss formula](/Users/cw/Documents/文库/2、网文
/medium/test/tmp_pic/pic_21.png)

    def huber_loss(true, pred, delta):
    huber_mse = 0.5 * np.square(true - pred)
    huber_mae = delta * (np.abs(true - pred) - 0.5 * (np.square(delta)))
    return np.where(np.abs(true - pred) <= delta, huber_mse, huber_mae)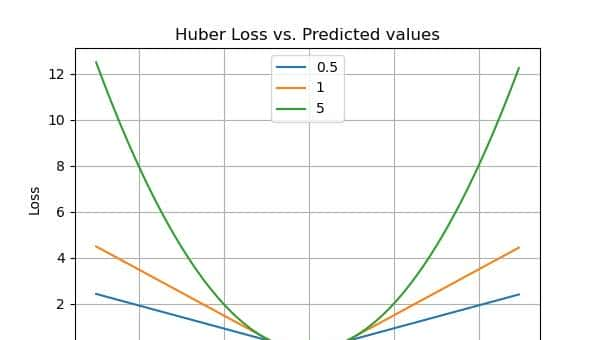

Huber损失评价指标的优点

• 它在零处可微分。
• 异常值由于在增量以上的线性关系得到了适当处理。
• 超参数， 可以调整以最大化模型的准确性。

Huber损失评估指标的缺点

• 额外的条件和比较使得Huber损失在处理大数据集时计算成本高昂。
• 为了最大化模型准确性， 需要被优化，并且这是一个迭代过程。
• 它仅可微分一次。

对数余弦损失

Log cosh计算误差的双曲余弦的对数。该函数比平方损失更平滑。它的工作方式类似于均方误差，但不受大预测误差的影响。在某种意义上，它与Huber损失超级类似，由于它是线性和平方评分方法的组合。

![](/Users/cw/Documents/文库/2、网文
/medium/test/tmp_pic/pic_23.png)

    def log_cosh(true, pred):
    logcosh = np.log(np.cosh(pred - true))
    logcosh_loss = np.sum(logcosh)
    return logcosh_loss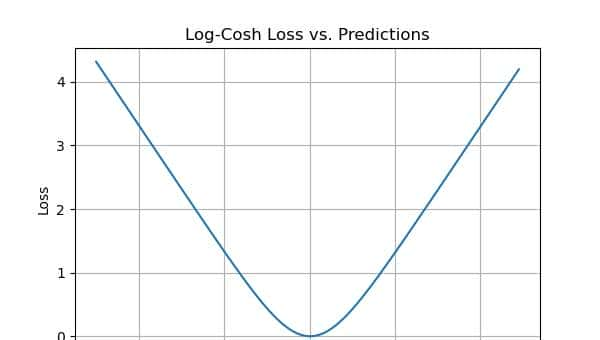

Log Cosh Loss评估指标的优点

• 它具有Huber损失的优点，同时在任何地方都是二次可微的。一些优化算法，如XGBoost，偏爱二次导数函数，而像Huber这样的函数只能一次可微。
• 它所需的计算比Huber少。

Log Cosh Loss 评估指标的缺点

• 它的适应性较差，由于它遵循固定的比例。
• 与Huber损失相比，推导更复杂，需要更深入的研究。

分位数损失

分位数回归损失函数用于预测分位数。分位数是决定组中有多少值低于或高于某个限制的值。它估计响应（因变量）相对于预测（自变量）变量的条件中位数或分位数。损失函数是MAE的扩展，除了50百分位数外，它是MAE。即使对于具有非恒定方差的残差，它也提供预测区间，并且不假定响应具有特定的参数分布。

γ表明所需的分位数。分位数值根据我们希望如何权衡正误差和负误差而选择。与线性回归模型中使用的平方差损失不同，该损失函数基于绝对差异。

损失函数

在上述损失函数中，γ 的值介于 0 和 1 之间。当出现低估时，公式的第一部分将主导；而在高估时，第二部分将主导。选定的分位数(γ)为过度预测和低估提供不同的惩罚。当 γ = 0.5 时，低估和高估受到一样因素的惩罚，并获得中位数。当 γ 的值增大时，高估的惩罚大于低估。例如，当 γ = 0.75 时，模型将惩罚高估，其成本是低估的三倍。基于梯度下降的优化算法从分位数中学习，而不是均值。

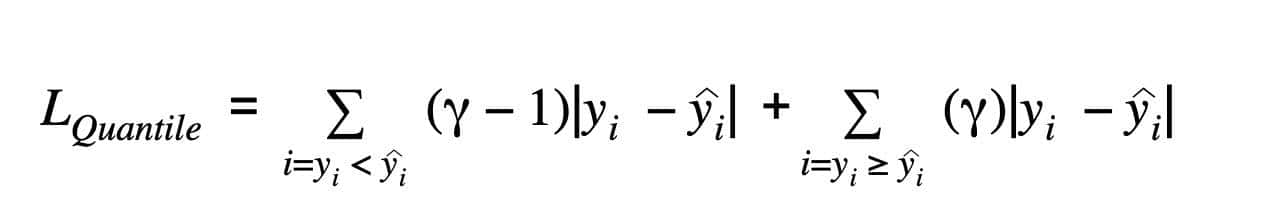
表明所需的分位数。分位数值是基于我们希望如何权衡正负误差而选择的。

在上述损失函数中， 的值在 0 和 1 之间。当存在低估时，公式的第一部分将占主导，而对于高估，第二部分将占主导。选择的分位数()为高预测和低预测提供了不同的惩罚。当 = 0.5 时，低估和高估将受到一样因素的惩罚，并且得到中位数。当 的值更大时，高估的惩罚将超过低估。例如，当 = 0.75 时，模型将对高估进行惩罚，其成本将是低估的三倍。基于梯度下降的优化算法从分位数而不是均值中学习。

    def quantile_loss(true, pred, gamma):
    val1 = gamma * np.abs(true - pred)
    val2 = (1-gamma) * np.abs(true - pred)
    q_loss = np.where(true >= pred, val1, val2)
    return q_loss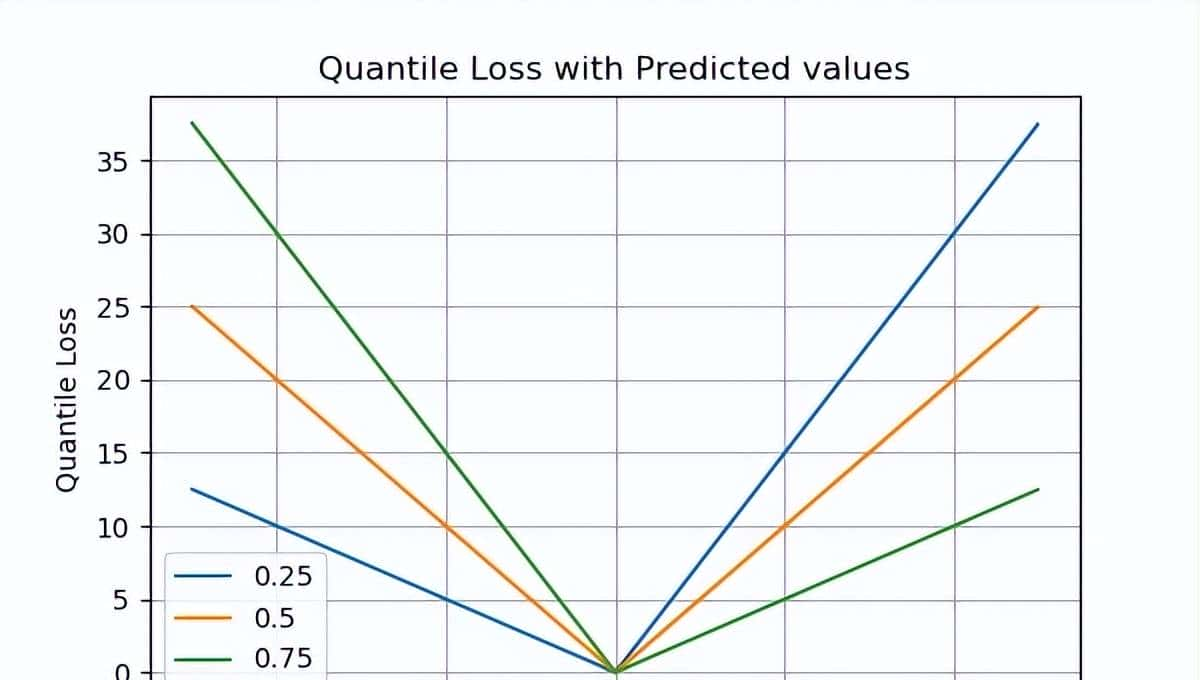

Quantile损失评估指标的优点

• 当我们预测区间而不是点估计时，它特别有用。
• 该函数也可以用于计算神经网络和基于树的模型中的预测区间。
• 它对异常值具有鲁棒性。

分位数损失评估指标的缺点

• 分位数损失计算量大。
• 如果我们使用平方损失来衡量效率或者我们要估计均值，那么分位数损失会更差。

结论

该综合指南探索了多种回归损失函数，阐明了它们的应用、优点和缺点。本文揭示了诸如 MAE、MBE、RAE、MAPE、MSE、RMSE（均方根误差）、RSE、NRMSE、RRMSE 和 RMSLE 等复杂指标，并介绍了专门的损失函数，如 Huber、Log Cosh 和 Quantile。它强调了影响损失函数选择的细微因素，从算法类型到异常值处理。此外，还涵盖了决定系数（R-平方）和来自 sklearn.metrics 的 r2_score 函数，以及调整后的 R-平方，它们是评估机器学习算法在回归问题中表现的重大评估指标。

感谢您阅读到这里！我希望这篇文章对您的学习旅程有所协助。我很想在评论中听到您提到的我遗漏的任何其他损失函数。祝评估愉快！

关键要点

• 损失函数对于比较预测值与实际值以完善回归模型至关重大。
• 平均绝对误差 (MAE) 的计算简单，并且能很好地处理异常值，但在零点不可微。
• 均方误差（MSE）对异常值敏感，并且由于平方的缘由，对较大错误的惩罚更重。
• 均方根误差 (RMSE) 提供了模型准确性的直观度量，并且易于解释。
• 高级指标如Huber损失和对数双曲余弦损失结合了MAE和MSE的特性，以实现对异常值的稳健处理。