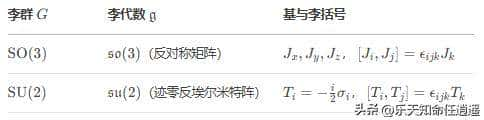
李群、李代数与伴随表示

1. 李群 (Lie Group)

定义：同时是光滑流形和群的结构，群运算（乘法、取逆）光滑。

群表明就是我们熟知的 3P 结构, 简记为 (G,V,R):

[群 G ] [表明空间 V 上的一般线性群 GL(V) ] 与 [同态映射 R ].
同态映射的同态指的是保群乘法: R(gαgβ)=R(gα)R(gβ), gα,gβ∈G.
核心特性：

描述连续对称性（如旋转、平移）。

局部由李代数生成，全局可能有拓扑复杂性（如 SU(2) 双覆盖 SO(3)）。

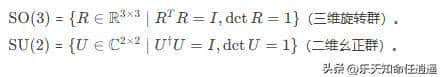
李群既是一个群，又是一个微分流形，能够在群操作下保持光滑结构。由于它是一个光滑的流形，因此可以利用微积分对其进行研究。

李群理论的核心思想就是利用李群的线性化版本来替换全局目标李群。这种局部或线性化表明被M.S.Lie称之为无穷小群，也就是李代数。

李代数是描述无穷小变换时用到的代数结构。李代数是李群在单位元处的切空间，它能够完全捕获李群的局部结构。一般而言可以将李代数中的元素看做是李群中无限接近于单位元的李群元素。

有了李代数的概念，李群能够内看成是局部拓扑等价于向量空间，那这样就可以将向量空间（线性空间）的模型和算法移植到李空间。

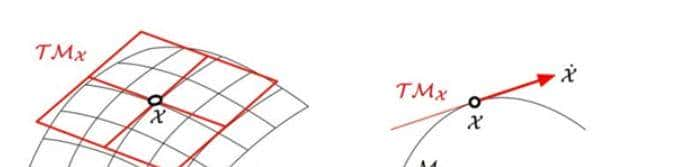
李群和李代数之间的相互转换，使得许多非线性空间问题能够利用李群表明成李代数结构，形成线性空间，这就为非线性问题的线性化表明找到了新的途径，除了利用线性特性构建统计模型之外，李代数还允许沿着李群流形上两点间的最短路径（测地线）引导物体，并且对变换能够给出自然的参数化表明。

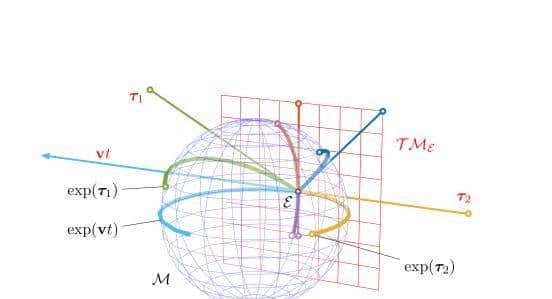
李群和李代数关系图

红色平面:李代数TMε,李群流形M(蓝色球部分)在单位元ε的切空间;李代数在原点ε产生的一条线性路径Vt通过指数映射exp(vt)与流形上的测地线对应.反之亦然:李群群元素测地线与李代数的向量一一对应.

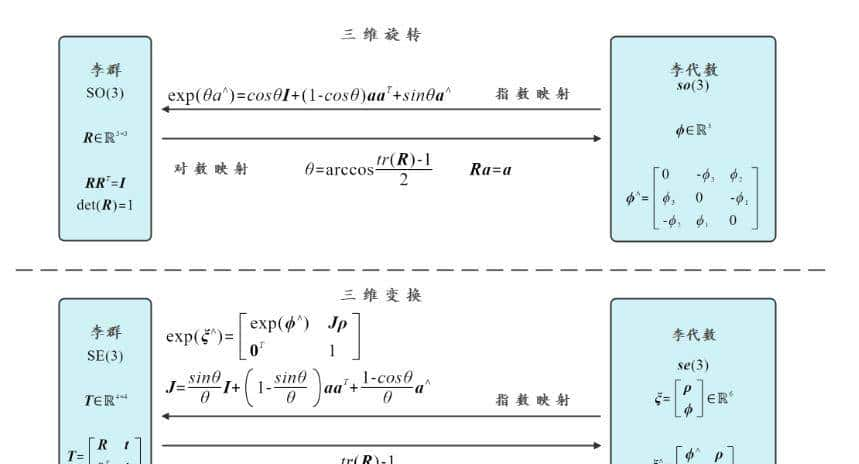
2. 李代数 (Lie Algebra)

李代数的表明也是一个 3P 结构, 简记为 (g,V,R):

[李代数 g] [表明空间 V 上的线性变换集合 End(V)] 与 [线性同态映射 R].
线性同态映射的同态指保李括号: R([X,Y])=[R(X),R(Y)], X,Y∈g.
其中等号左边的李括号是李代数里的矢量乘法, 右边的李括号是矩阵对易子.

定义：李群在单位元 e 处的切空间，装备李括号 [X,Y]满足：

双线性 :∀ X , Y , Z ∈ g , a , b ∈ V , 有

[aX+bY,Z]=a[X,Z]+b[Y,Z],

[Z,aX+bY]=a[Z,X]+b[Z,Y].

反对称： [X,Y]=−[Y,X]

自反性 :[X,X]=0.

雅可比恒等式： [X,[Y,Z]]+[Y,[Z,X]]+[Z,[X,Y]]=0

数学结构：

向量空间 g + 李括号 [⋅,⋅]:g×g→g。

通过指数映射生成群： exp⁡(tX)∈G（X∈g, t∈R)。

几何意义：

g 的元素是无穷小生成元（如角速度矢量 ω)。

李括号 [X,Y]衡量群乘法的非交换性。

3. 伴随表明 (Adjoint Representation)

定义：李群 G在其李代数 g上的一个线性表明,就是这个李群的伴随表明.

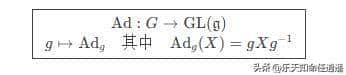
gXg−1∈g 证明:

单参子群 gx(t) 对 ∀g∈G 都可以生成新的单参子群 ggx(t)g−1.
新曲线过恒等元:

ggx(0)g−1=gx(0).
新曲线满足群乘法:

ggx(t1)g−1ggx(t2)g−1=ggx(t1+t2)g−1.
gy(t)≡ggx(t)g−1 就是一条全新的单参子群了.

将俩单参子群分别表达为

gx(t)=e^(itX),

gy(t)=e^(itY),

(可以参见李群与李代数关系图之Vt→exp(vt)…)然后:

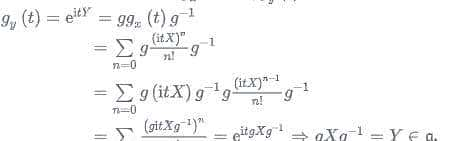
伴随表明 (G,g,ad) , 其中 ad:G→GL(g).

对 ∀g∈G 生成的 adg:g→g 作为线性变换显然都是 End(g) 中的元素,
而该映射又显然可逆, 故有 adg∈GL(g)⊂End(g).
这样就又找到了一个群 G 到一般线性群 GL(g) 的映射 ad:G→GL(g).
它是不是同态映射呢?
显然是的:

adgg′X=gg′Xg′−1g−1=g(adg′X)g−1=adgadg′X.
找到一个 G→GL(g) 的映射, 还保群乘法
李群的伴随表明都是自共轭表明.

李群伴随表明的维度就是对应流形的维度, 也是李代数的维度或独立生成元的个数.

微分版本（李代数的伴随表明）：

对 ∀X∈g 在此定义下生成的 adX 的确 是 g→g 的映射, 即 adX∈End(g).
其次, 这铁是个线性变换, 由于对 ∀c1,c2∈R, ∀X,Y,Z∈g 下式均成立:
adX(c1Y+c2Z)=[X,c1Y+c2Z]=c1adXY+c2adXZ.
这就是说 adX∈End(g).

所谓的伴随表明 (g,g,ad), 其中 ad:g→End(g).

雅可比恒等式证明:
ad[X,Y]Z=[[X,Y],Z]
=−[Z,[X,Y]]
=[X,[Y,Z]]+[Y,[Z,X]]
=[X,[Y,Z]]−[Y,[X,Z]]
=adXadYZ−adYadXZ=

（SU(2) 的伴随表明）：

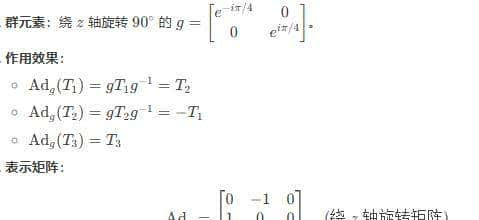
几何意义：Adg 是 g的线性自同构，对应群共轭作用 h↦ghg−1的微分。

物理意义：规范场（如胶子）按伴随表明变换

4. Wigner 定理与伴随表明的关系
   Wigner 定理（量子力学中的基本定理）指出：

任何保持量子态内积不变的对称变换

（即满足 |⟨ϕ|ψ⟩|=|⟨Uϕ|Uψ⟩| 的映射 U）必须是 酉算子 或 反酉算子。

在对称群 G 的酉表明下，生成元的变换由伴随表明刻画：
定理：设 U:G→U(H)是 G 的酉表明，其李代数表明为 dU:g→u(H)（厄米算子）。则对任意 g∈G 和 X∈g，有：

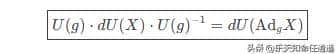
物理意义：

左边：群元素 g通过酉算子 U(g)共轭作用在生成元 dU(X)上。

右边：生成元被变换为 AdgX对应的算子，即李代数的伴随表明。

对称变换下，物理观测量的变换规律由李代数的伴随表明完全刻画。

例如：旋转群 SO(3) 中，角动量算符的变换等价于三维向量的旋转（即 AdR 的作用）。

此关系统一了量子对称性（Wigner 定理）与李群表明理论（伴随表明），是连接对称性、量子力学和几何变换的数学基础。