m基于GRNN广义回归神经网络和LLE特征提取的人脸情绪识别matlab仿真

1.算法描述

GRNN，即General Regression Neural Network，中文全称为广义回归神经网络，是由The Lockheed Palo Alto研究实验室在1991年提出的。GRNN是一种新型的基于非线性回归理论的神经网络模型。GRNN是建立在非参数核回归基础之上的，该神经网络是以测试样本为后验条件，并从观测样本中计算得到自变量和因变量之间的概率密度函数，然后在计算出因变量关于自变量的回归值。由于GRNN不需要规定模型的类型，只需要设置神经网络的光滑因子参数，GRNN神经网络的光滑因子参数的取值对神经网络的输出影响较大，当光滑因子参数较大的时候，其对应的神经元所覆盖的输入区域就越大；当光滑因子参数较小的时候，神经网络对应的径向基函数曲线较陡，因此神经网络输出结果更接近期望值，但此时光滑度越差。由于GRNN广义回归神经网络是基于非线性核回归分析的神经网络，因此，对于任意一个非独立变量y，其相对于独立变量x的回归分析的过程是计算具有最大致率值y。现假设随机变量x和y的联合概率密度函数为f (x ,y)，已知x的观测值为X，则y相对于X的回归，即条件均值为：

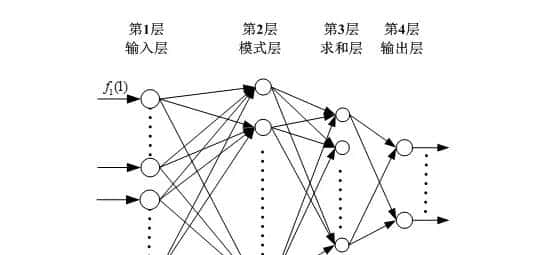
从图3的结构图可知，GRNN神经网络的输入层神经元数目和输入样本的维度是一样的，即每一个神经元将输入信号直接传递给GRNN神经网络的隐含层中。GRNN神经网络的模式层的神经元数目和学习训练样本的数目一样，即每一个神经元都分别对应着一个不同的学习训练样本.

2.仿真效果预览

matlab2022a仿真结果如下：

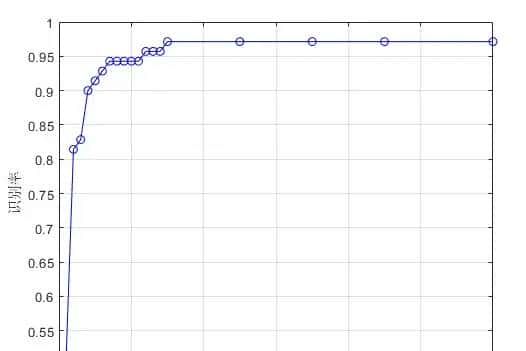
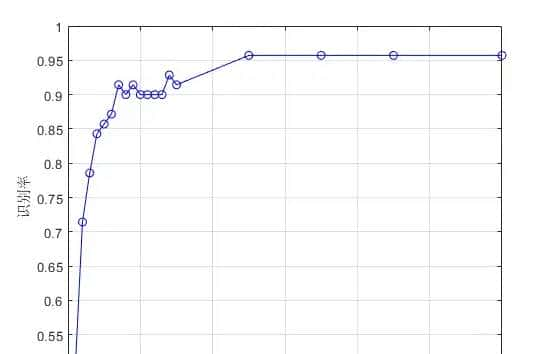
m基于GRNN广义回归神经网络和LLE特征提取的人脸情绪识别matlab仿真

对于测试集人脸样本的生气识别率为93.3333%

对于测试集人脸样本的厌恶识别率为96.6667%

对于测试集人脸样本的害怕识别率为93.3333%

对于测试集人脸样本的开心识别率为90%

对于测试集人脸样本的中性识别率为100%

对于测试集人脸样本的悲伤识别率为93.3333%

对于测试集人脸样本的惊讶识别率为100%

整体识别率为95.2381%

3.MATLAB核心程序

SET = [];

for flag = 1:3

flag

if SEL == 1

display( 读入训练集合… );

if TEST_DATA == 1

%第一组样本

TrainData = readfaceFeature(nExpressionPerPerson, nPerson,0,130);

trainLabel = [1,1,2,2,3,3,3,4,4,4,5,5,6,6,7,7,1,1,2,2,2,3,3,4,4,5,5,6,6,7,7,1,1,2,3,3,4,4,4,5,5,6,6,6,7,7,1,1,2,2,3,3,4,4,5,5,6,6,7,7,1,1,2,2,3,3,4,4,4,5,5,6,6,7,1,1,2,3,3,4,4,5,5,6,6,7,7,1,1,2,2,3,3,4,4,5,5,6,6,7,7,1,1,2,2,3,3,4,4,5,5,6,6,7,7,1,1,2,2,3,3,3,4,4,5,5,6,6,7,7] ;

%降低维度

%pcaFaces = fastPCA(TrainData,DIM); % 主成分分析PCA

pcaFaces = lle(TrainData ,12,DIM);

end

if TEST_DATA == 2

%第二组样本jaffe

TrainData0 = readfaceFeature2(nExpressionPerPerson, nPerson,0,140,flag);

trainLabel1 = [1,2,3,4,5,6,7,…

1,2,3,4,5,6,7,…

1,2,3,4,5,6,7] ;

trainLabel = [trainLabel1;trainLabel1];

%降低维度

%pcaFaces = fastPCA(TrainData,DIM); % 主成分分析PCA

pcaFaces = lle(TrainData0 ,12,DIM);

end

X = pcaFaces;

TrainData = X;

[X,A0,B0] = scaling(X);

%替换算法，使用GRNN神经网络，否则原来的SVM我仔细研究下来，缺陷太大，几次改下来，性能也没到50%，所以选择pass

%但为了你方便写论文，我在文档中将GRNN神经网络的理论都给你写了，然后测试大致也写了，

net = multiGRNNTrain(TrainData ,trainLabel ,0.0015);

save NN_model.mat net A0 B0

display( ………………………… );

display( 训练结束。 );

end

display( 读入测试集合… );

%降低维度

load NN_model.mat

load PCA.mat

load LLE.mat

if TEST_DATA == 1

%第一组样本

TestData0 = readfaceFeature(nExpressionPerPerson, nPerson,1,130);

TestLabel = [1,1,2,2,3,3,3,4,4,4,5,5,6,6,7,7,1,1,2,2,2,3,3,4,4,5,5,6,6,7,7,1,1,2,3,3,4,4,4,5,5,6,6,6,7,7,1,1,2,2,3,3,4,4,5,5,6,6,7,7,1,1,2,2,3,3,4,4,4,5,5,6,6,7,1,1,2,3,3,4,4,5,5,6,6,7,7,1,1,2,2,3,3,4,4,5,5,6,6,7,7,1,1,2,2,3,3,4,4,5,5,6,6,7,7,1,1,2,2,3,3,3,4,4,5,5,6,6,7,7] ;

[m,n] = size(TestData0);

TestData = (TestData0-repmat(meanVec, m, 1))*V; % 经过pca变换降维

end

if TEST_DATA == 2

%第二组样本jaffe

TestData0 = readfaceFeature2(nExpressionPerPerson, nPerson,1,70,flag);

TestLabel = [1,2,3,4,5,6,7,…

1,2,3,4,5,6,7,…

1,2,3,4,5,6,7] ;

[m,n] = size(TestData0);

TestData = (TestData0-repmat(meanVec, m, 1))*V; % 经过pca变换降维

end