初中实数的乘方与开方及其运算指导

一、认识实数：基础回顾

1. 实数的定义

– 包含有理数（整数、分数）和无理数（无限不循环小数，如√2 , π ）。

2. 数轴上的实数

– 所有实数均可对应数轴上的唯一一点，反之亦然。

二、乘方：幂的运算

1. 乘方的定义

– 概念：将一样因数连乘的运算称为乘方，记作 aⁿ 。

– a 是底数（实数）

– n 是指数（正整数）

– 结果称为 a 的 n 次幂。

– 示例：

5³ = 5×5×5 = 125

(-2)⁴ = (-2)×(-2)×(-2)×(-2) = 16

2. 乘方的性质与法则

3. 易错点提醒

– 区分符号位置：

-2⁴ = -(2⁴) = -16

(-2)⁴ = 16

– 0的乘方： 0ⁿ = 0 （ n≥1 ）， 0⁰ 无意义。

三、开方：平方根与算术平方根

1. 平方根的定义

– 若 x² = a （ a ≥ 0 ），则 x 是 a 的平方根。

– 性质：

– 正数有两个平方根，互为相反数（如 √9 = 3 ， -√9 = -3 ）；

– 0的平方根是0；

– 负数没有实数平方根。

2. 算术平方根

– 定义：正数 a 的正平方根，记作 √a （读作“根号a”）。

– 性质：

– √a ≥ 0 （结果非负！）

– (√a)² = a （ a ≥ 0 ）

– 示例：

√16 = 4 ， √0 = 0

3. 立方根

– 若 x³ = a ，则 x 是 a 的立方根，记作 ∛a 。

– 性质：

– 正数有正立方根，负数有负立方根；

– ∛(-a) = -∛a 。

– 示例：

∛8 = 2 ， ∛(-27) = -3

四、乘方与开方的综合运算

1. 运算优先级规则

> 括号 → 乘方/开方 → 乘除 → 加减

– 示例：

3 + √16 × 2² = 3 + 4 × 4 = 3 + 16 = 19

2. 常见运算类型与技巧

3. 估算开方结果

– 步骤：

1. 确定相邻的完全平方数（如 4²=16 < 20 < 25=5² ）；

2. 在 4 和 5 之间估算 √20 ≈ 4.47 （可通过计算 4.5²=20.25 调整）。

五、典型例题精析

1. 计算： (-3)² × ∛8 + √25

解：

= 9 × 2 + 5

= 18 + 5 = 23

2. 比较大小： √10 与 3.1

解：

(√10)² = 10 ， 3.1² = 9.61 → 10 > 9.61 → √10 > 3.1

六、避坑指南（常见错误总结）

1. 混淆 (-a)ⁿ 与 -aⁿ → 牢记括号的作用；

2. 忽略算术平方根的非负性 → √a ≥ 0 ；

3. 开方后漏解 → 正数平方根有两个（一正一负）；

4. 运算顺序错误 → 严格遵循优先级规则。

七、知识框架图

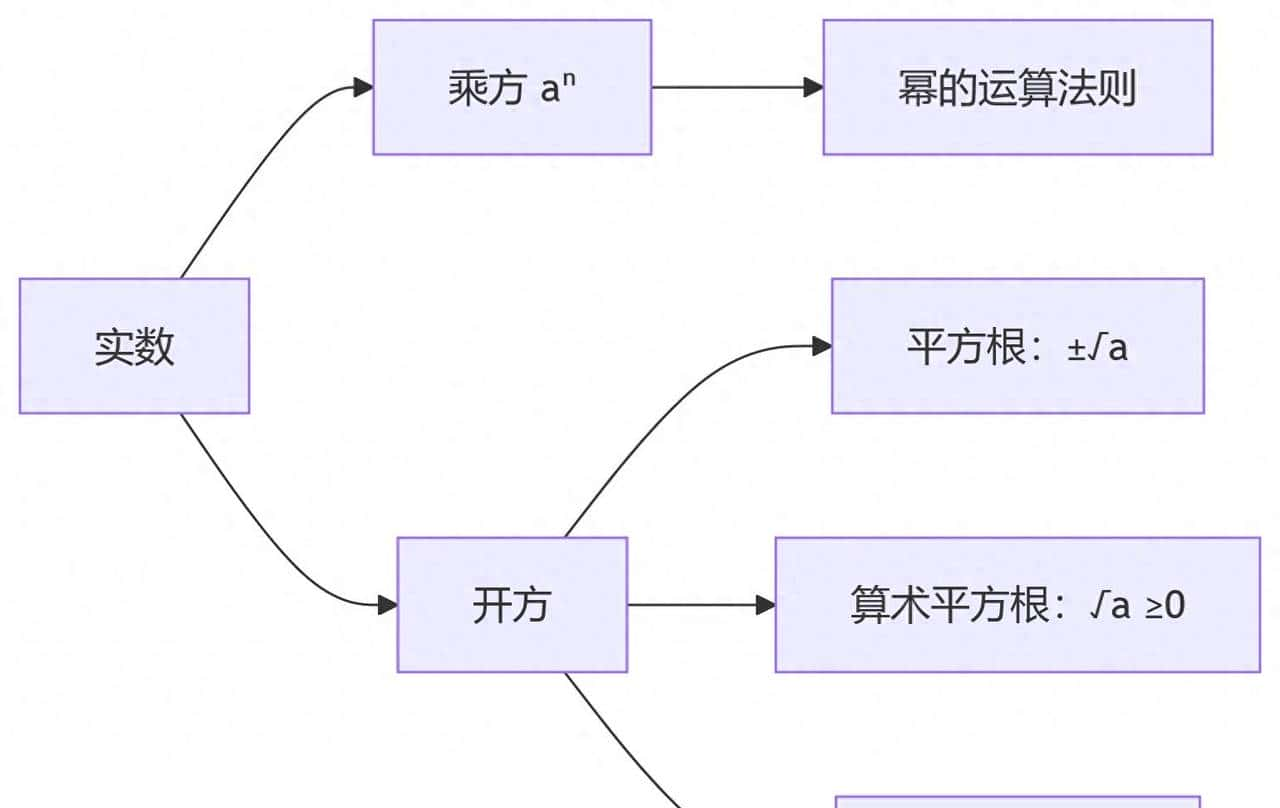
结语：乘方与开方是实数运算的核心工具，理解定义、掌握法则、熟练运用优先级规则，是解决复杂问题的基石。勤练典型例题，规避常见错误，数学能力必将稳步提升！

说明：

– 适用对象：初中七年级至九年级学生

– 重点标注：公式、性质、易错点

– 提议使用：可作为课堂笔记、复习讲义或自学材料