深层网络的梯度消失问题，本质是 “反向传播时，梯度信号经过多层后被严重削弱，导致浅层参数几乎无法更新”。残差连接通过一个精妙的设计，给梯度信号开辟了 “直达通道”，从根本上缓解了这个问题。

先理解：梯度消失为什么会发生？

神经网络训练时，参数更新依赖 “梯度”—— 损失函数对参数的偏导数。这个梯度需要从输出层反向传播到输入层（列如从第 12 层传到第 1 层）。

没有残差连接时，每层的梯度计算都要 “乘以该层的权重导数”。就像多米诺骨牌，每一块倒下的力度（梯度）都会被下一块 “削弱”：

• 假设每层的权重导数平均是 0.5，经过 10 层后，梯度就只剩初始值的 0.5¹⁰≈0.00098（几乎消失）
• 传到浅层时，梯度已经接近 0，参数几乎无法更新，模型自然学不到东西

这就像用一根长水管浇水，每节水管都漏水，到最前面时几乎没水了 —— 梯度就是那 “水”，浅层参数就是 “最前面需要浇水的植物”。

残差连接的 “梯度保护魔法”：给梯度加条 “高速路”

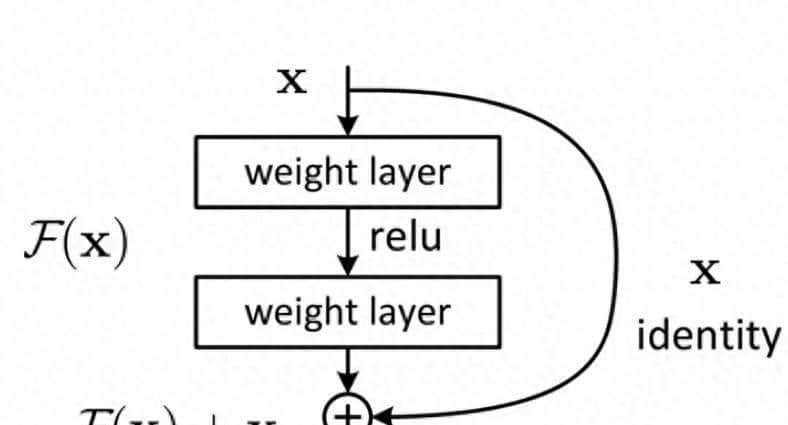
残差连接的核心公式是：残差块输出 = 输入 + 层的计算结果（即 H (x) = F (x) + x），其中：

• x 是残差块的输入
• F (x) 是该层通过卷积 / 全连接等操作学到的 “差异信息”（残差）
• H (x) 是残差块的输出

这个简单的 “加法”，在反向传播计算梯度时会产生神奇效果：

根据微积分的 “加法求导法则”，损失函数 L 对 x 的梯度为：
∂L/∂x = ∂L/∂H(x) × ∂H(x)/∂x = ∂L/∂H(x) × (∂F(x)/∂x + 1)

这个公式里藏着关键：梯度被分成了两部分：

1. 通过 F (x) 传递的梯度：∂L/∂H (x) × ∂F (x)/∂x（可能衰减的部分）
2. 直接传递的梯度：∂L/∂H (x) × 1（不衰减的部分）

为什么这能解决梯度消失？

想象梯度从深层（列如第 12 层）传到浅层（列如第 1 层）：

• 没有残差连接时，梯度需要经过 12 次 “权重导数相乘”，很容易衰减到接近 0
• 有残差连接时，每一层的梯度都包含一个 “+1” 的项 —— 这意味着梯度可以不经过 F (x) 的复杂计算，直接 “跳” 过该层传递！

即使 F (x) 的梯度（∂F (x)/∂x）很小甚至接近 0，整体梯度（∂L/∂x）也至少等于 ∂L/∂H (x)（由于 0 + 1 = 1）。梯度不会被 “完全吞噬”，而是能以较强的信号传递到浅层。

打个比方：
没有残差连接的梯度传播，像走 “布满碎石的山路”，每一步都有损耗；
有残差连接时，相当于在山路旁修了 “高速公路”（那个 + 1 的项），大部分梯度可以走高速，损耗极小。

直观例子：100 层网络的梯度变化

假设我们有一个 100 层的网络：

• 有残差连接：每层梯度至少保留 1（来自 + 1 项），即使 F (x) 部分衰减到 0，100 层后梯度依然等于初始值 —— 浅层参数能收到清晰的更新信号

这就是为什么有了残差连接，我们才能训练几十甚至上百层的 Transformer—— 梯度不再 “迷路”，深层网络终于能 “从头到脚” 都得到有效训练。

总结：残差连接的核心贡献

残差连接通过 “输出 = 输入 + 学习到的差异” 的设计，在反向传播时为梯度提供了一条 “不衰减的直接路径”。即使网络很深，梯度也能稳定传递到浅层，从根本上解决了 “梯度消失导致浅层参数无法更新” 的难题。这就像给深层网络的梯度传递装上了 “信号放大器”，让复杂模型的训练从 “不可能” 变成了 “可能”。