24252自动控制原理第二章连续系统的数学模型

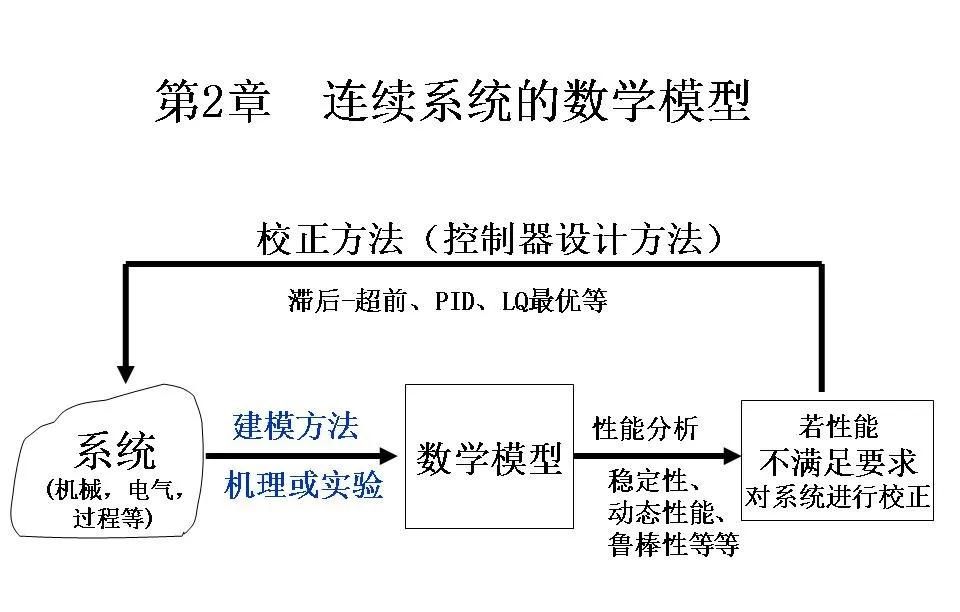
热烈欢迎王老师的自动控制原理课程上线斐之学堂公众号，本期推出第二章连续系统的数学模型，敬请大家一起学习，共同进步。

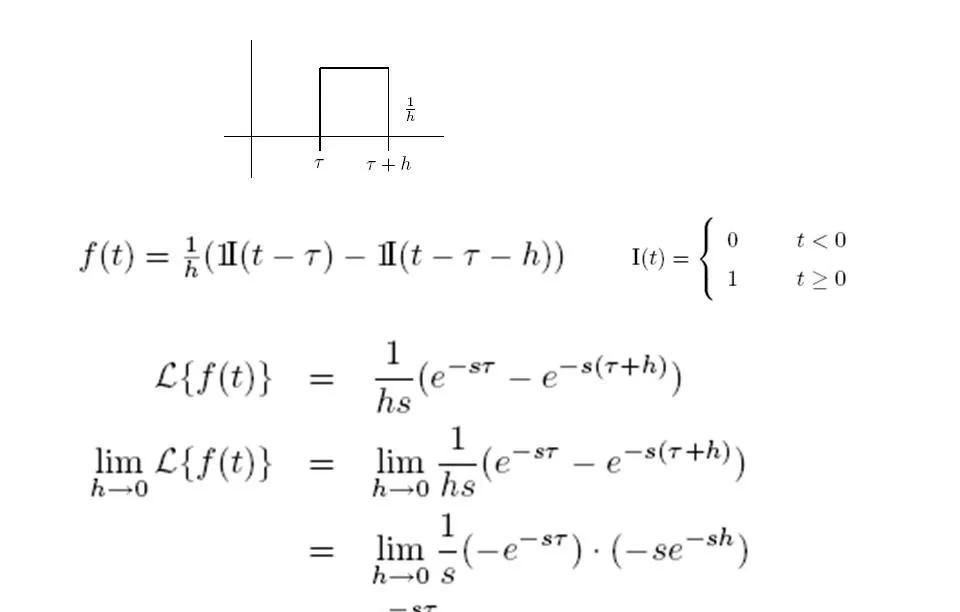
知识点聚焦：

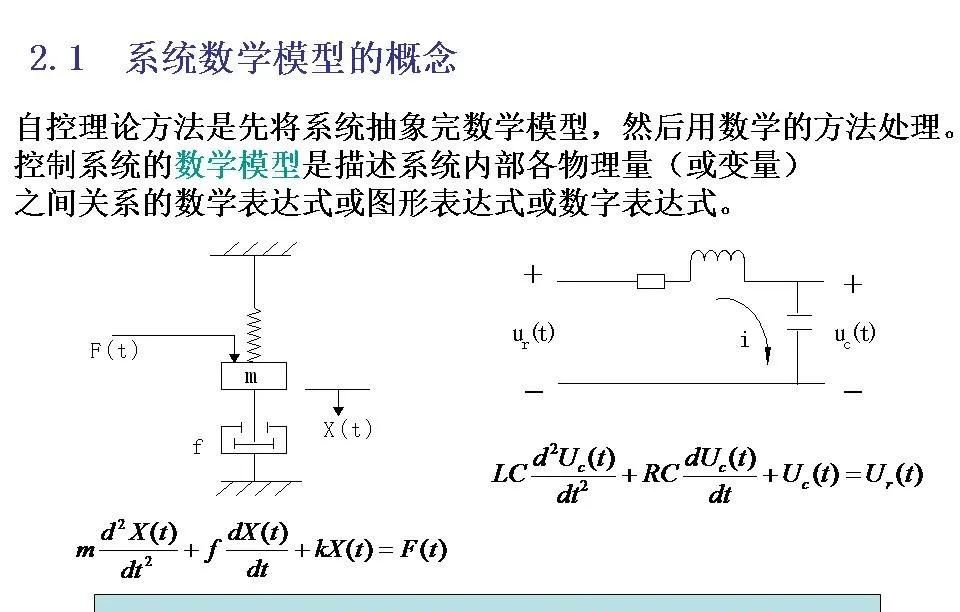
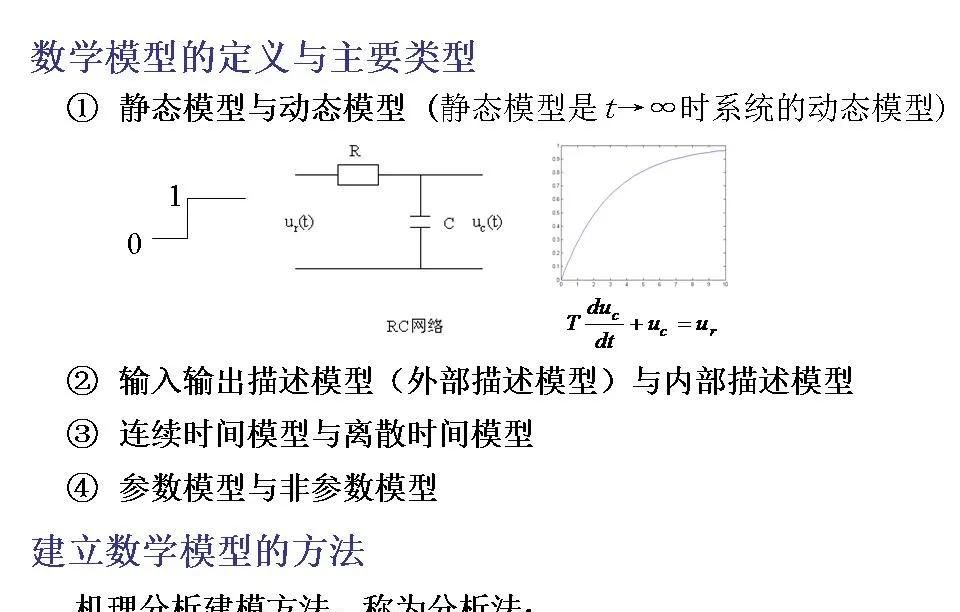
1数学模型的概念

数学模型是指使用数学语言和工具对现实世界中的现象、系统或过程进行描述的一种抽象表达。它通过一组数学方程（如代数方程、微分方程、差分方程等）来模拟实际问题，从而可以用于分析、预测和优化这些系统的性能。

数学模型的构成要素

变量（Variables）：

描述系统状态的量，可以是输入变量、输出变量或者内部状态变量。它们可能是时间的函数（连续时间系统）或者是离散时刻上的值（离散时间系统）。

参数（Parameters）：

定义系统特性的常数值，例如物理系统的质量、阻尼系数等。参数一般反映了系统内在属性或外部条件的影响。

方程（Equations）：

用来表明变量之间关系的一组公式，包括但不限于线性方程、非线性方程、微分方程、积分方程等。根据问题的性质，可以是静态方程（不涉及时间变化）或是动态方程（随时间变化）。

约束条件（Constraints）：

系统运行时必须满足的限制条件，列如资源限制、物理定律等。这些条件可能会以边界条件、初始条件等形式出现。

数学建模的过程

问题定义：明确要解决的问题是什么，确定研究对象及其边界。

假设设定：基于实际情况提出合理的简化假设，以便于构建模型。这一步骤对于简化复杂问题至关重大。

选择适当的数学结构：根据问题的特点选取合适的数学框架，如概率论、图论、线性代数等。

建立模型：利用选定的数学工具构造出能够反映问题本质的方程组。

求解与验证：通过解析方法或数值计算找到模型的解，并将结果与实际情况对比检验其合理性。

模型改善：根据验证过程中发现的问题调整假设或修改模型，直到获得满意的结果为止。

数学模型的应用领域

数学模型广泛应用于各个学科和技术领域，包括但不限于：

自然科学：物理学、化学、生物学等领域中用来解释自然规律。

工程技术：自动控制、机械工程、电气工程等中用于设计和优化系统。

社会科学：经济学、社会学等中用以研究人类行为和社会结构。

医学健康：疾病传播模型、药物动力学等。

环境科学：气候变化预测、生态系统保护等。

总之，数学模型是连接理论与实践的重大桥梁，它不仅协助我们理解复杂的现实世界，也为决策提供了有力的支持。在科学研究和技术开发中扮演着不可或缺的角色。

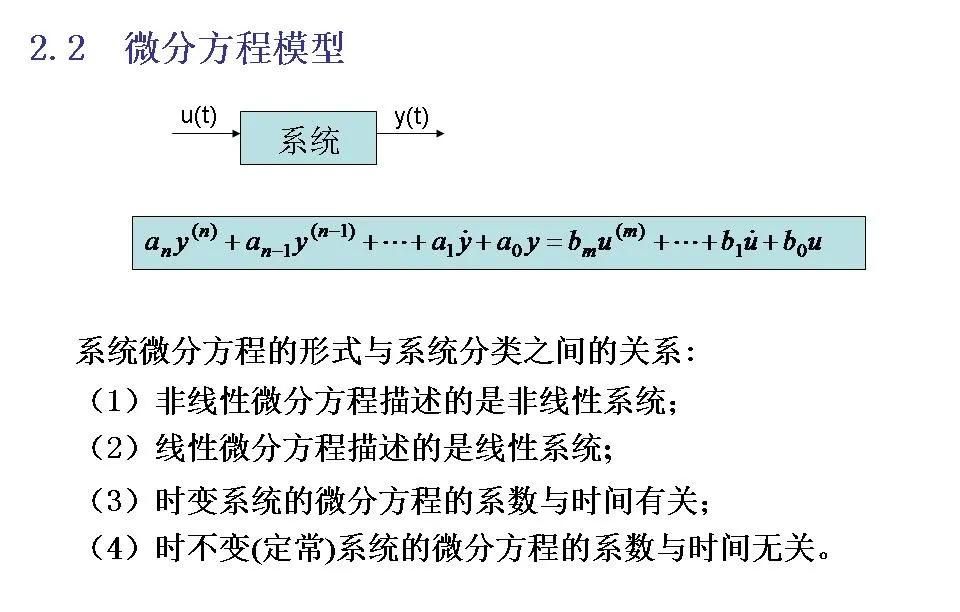
2建立控制系统微分方程的方法

建立控制系统微分方程是分析和设计自动控制系统的基石。以下是几种常见的方法来建立描述控制系统的微分方程：

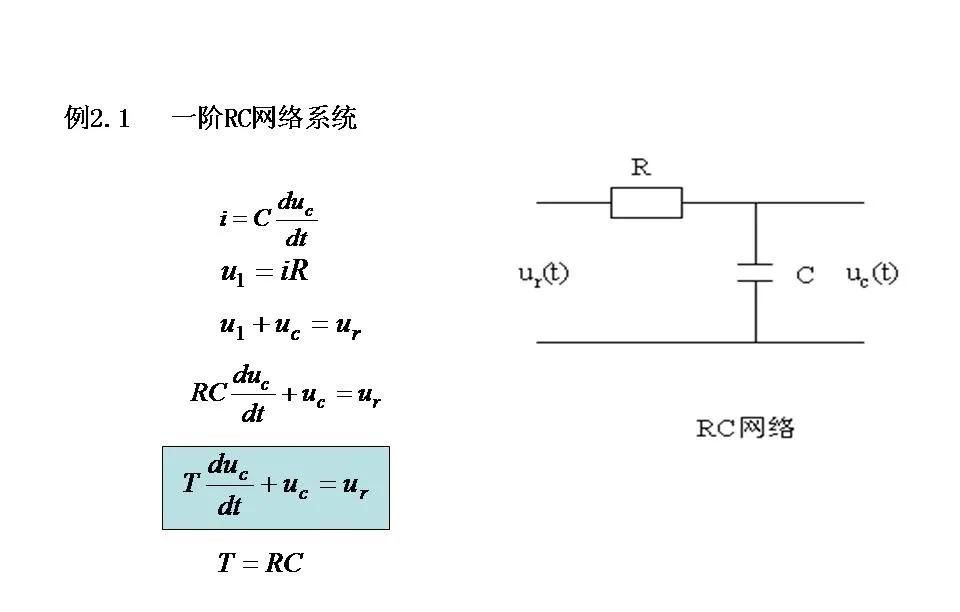
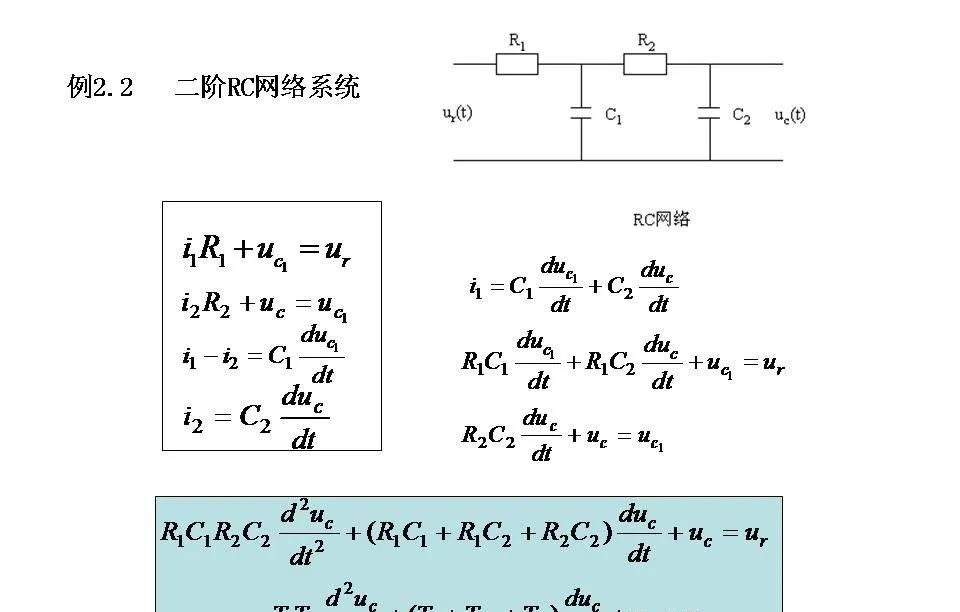
1. 物理定律法

根据物理、化学或生物等基本定律，如牛顿第二运动定律、热力学第必定律、基尔霍夫电流电压定律等，直接推导出系统的数学模型。这种方法适用于可以明确知道其内部机制的系统。

机械系统：利用牛顿定律或其他动力学原理。

电气系统：应用基尔霍夫定律以及元件（电阻、电感、电容）的电压-电流关系。

热力学系统：使用能量守恒原则。

2. 状态空间表明法

状态空间方法是一种用一组一阶微分方程来描述高阶系统的通用方式。它定义了系统的状态变量，并通过这些变量之间的关系来表达系统的动态行为。

选择状态变量：确定能够完全描述系统行为的最小数目的一组变量。

写出状态方程：对于每个选定的状态变量，写出一个关于时间的一阶微分方程。

输出方程：如果需要的话，还要写出将状态变量与实际测量输出联系起来的代数方程。

3. 拉普拉斯变换法

拉普拉斯变换是一种从时域转换到复频域的方法，它可以使线性常系数微分方程转化为简单的代数方程，从而简化求解过程。完成求解后再逆变换回时域得到原问题的答案。

对微分方程进行拉普拉斯变换：将初始条件思考进去。

求解变换后的代数方程：一般更容易处理。

执行拉普拉斯逆变换：获得原始时域中的解。

4. 黑箱建模（数据驱动建模）

当系统的内部结构未知或者难以用物理定律准确描述时，可以采用黑箱建模的方法。这主要依赖于输入输出数据来识别系统的动态特性，列如通过自回归移动平均模型（ARMA）、神经网络或者其他机器学习算法来进行建模。

收集实验数据：获取系统的输入输出样本。

选择合适的模型结构：例如传递函数、状态空间模型等。

参数估计：使用最小二乘法、极大似然估计等技术来确定模型参数。

5. 组合建模

有时候单个组件的模型是已知的，但整个系统的模型却不是。在这种情况下，可以通过组合各个子系统的模型来构建整个系统的微分方程。例如，在多体动力学中，就是把多个刚体的运动方程结合起来形成整体的系统方程。

6. 数值模拟

在某些复杂的情况下，解析地建立和求解微分方程可能是不切实际的。此时，可以采用数值模拟的方法，如有限元分析（FEA）、计算流体力学（CFD）等，这些方法可以在计算机上近似地解决问题并提供有用的洞察。

每种方法都有其适用范围和局限性，工程师和技术人员会根据具体情况选择最合适的方法。在实践中，往往是多种方法结合使用，以充分利用各自的优势。

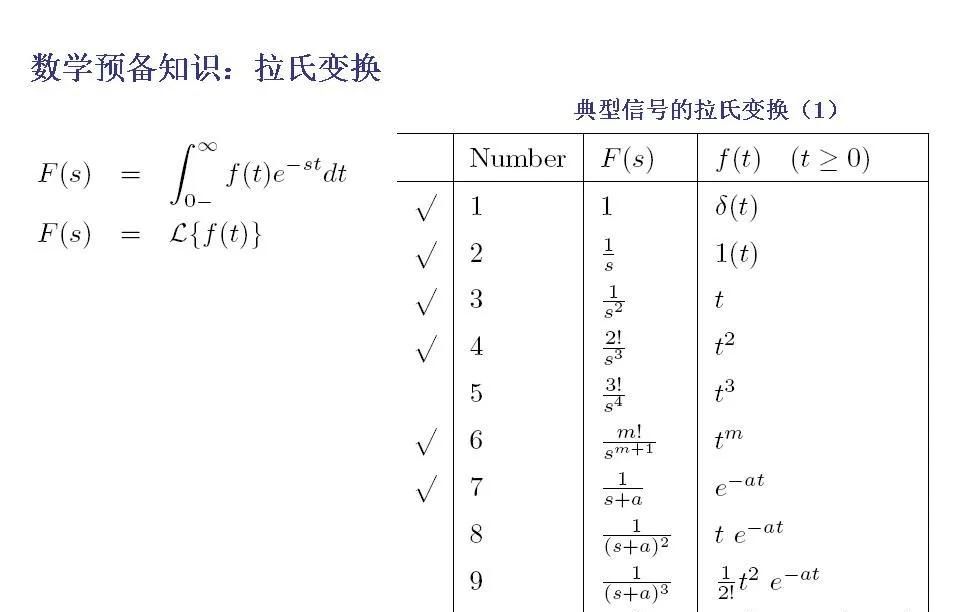
3拉普拉斯变换

拉普拉斯变换（Laplace Transform）是一种数学工具，主要用于求解线性微分方程和积分方程。它将一个时间域中的函数转换为复频域中的函数，从而简化了问题的求解过程。拉普拉斯变换广泛应用于工程学、物理学以及自动控制理论等领域。要熟练掌握拉普拉斯变换的定义和性质。

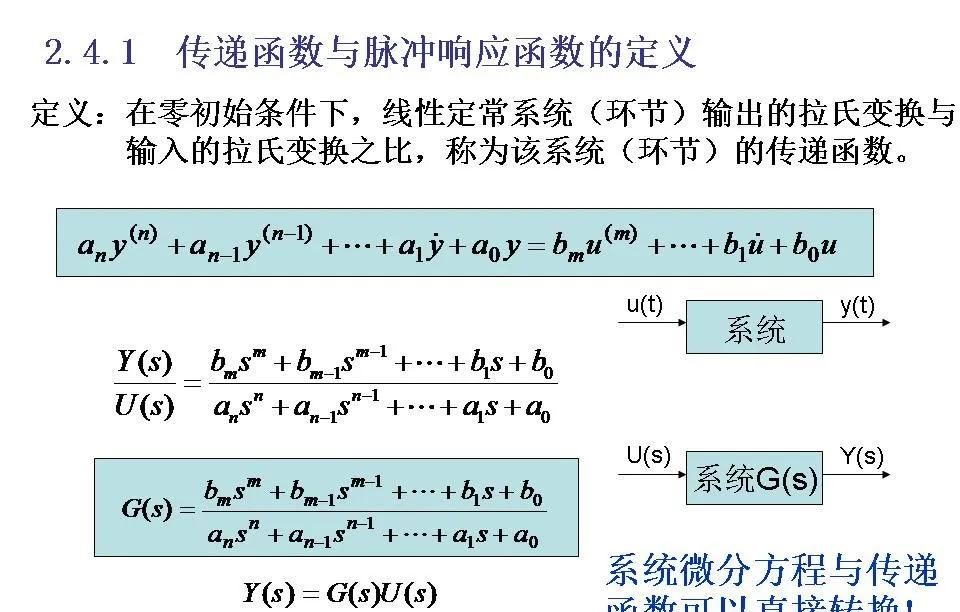
4传递函数

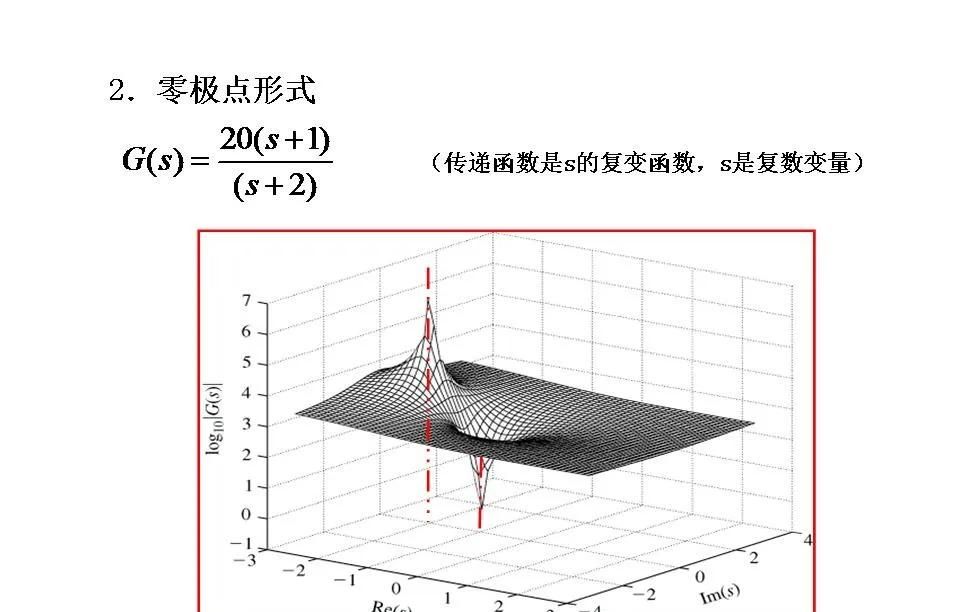
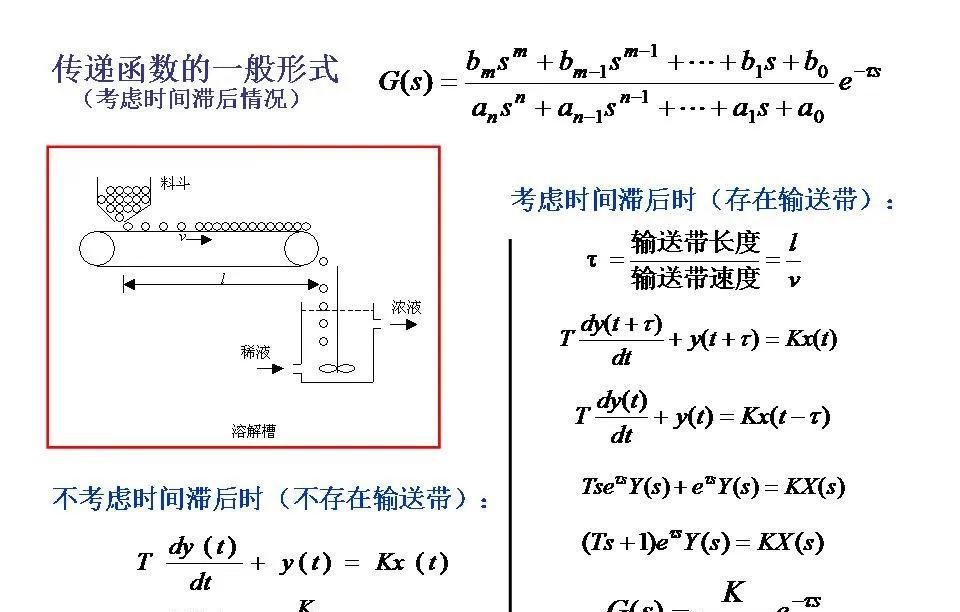
传递函数（Transfer Function）是线性时不变系统（LTI system）中的一种数学模型，它描述了系统的输出与输入之间的关系。具体来说，传递函数定义为在零初始条件下，系统输出的拉普拉斯变换与输入的拉普拉斯变换之比。熟练掌握传递函数的定义和性质。

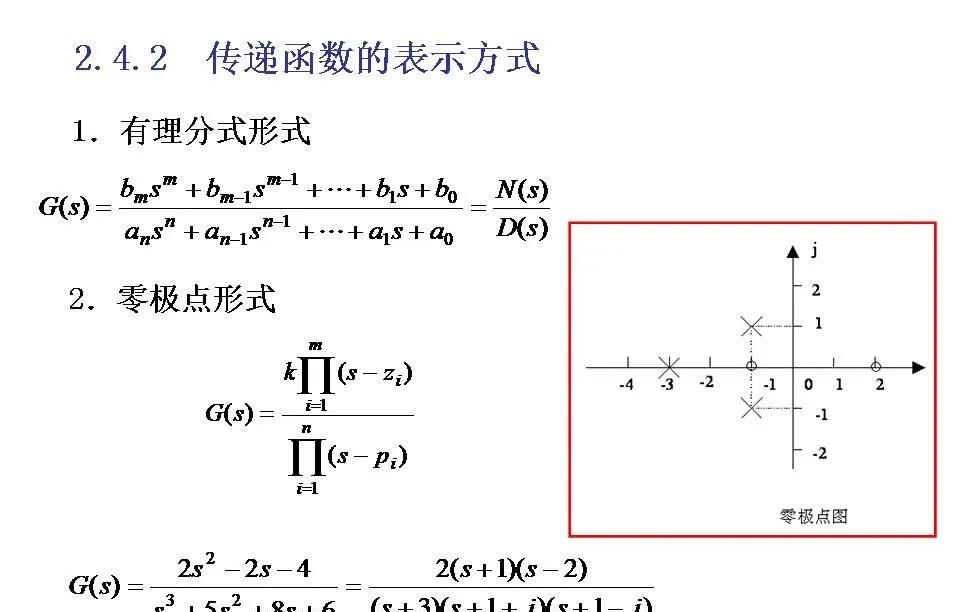
稳定性指示：

系统的稳定性可以从传递函数的极点位置来判断。如果所有极点都在复平面的左半部分，则系统稳定；如果有任何一个极点位于右半平面或虚轴上（除了原点），则系统不稳定或临界稳定。

简化微分方程：

传递函数能够将复杂的高阶微分方程转换成简单的代数表达式，从而使得求解过程更为简单。

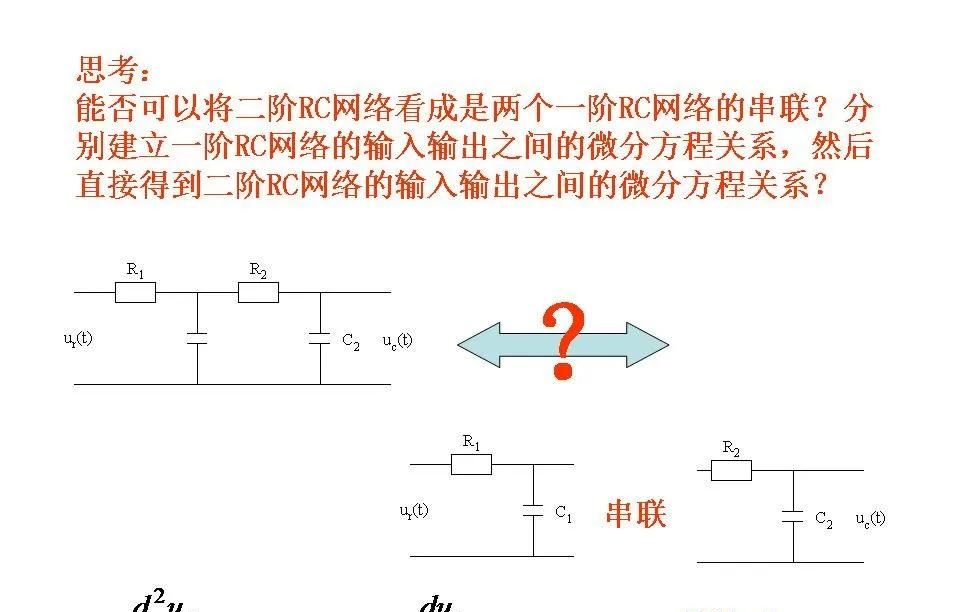
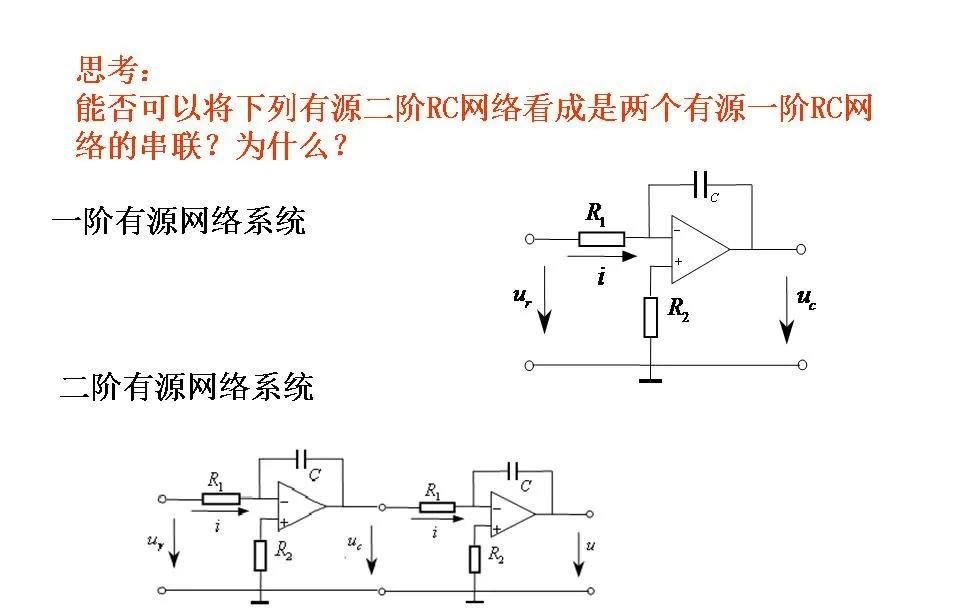
级联和并联系统：

对于由多个子系统串联组成的复合系统，其总传递函数等于各个子系统传递函数的乘积。

对于并联连接的子系统，总传递函数是各子系统传递函数的和。

BIBO稳定性：

一个系统如果是有界的输入导致有界的输出（BIBO, Bounded Input Bounded Output），那么这个系统被认为是稳定的。对于传递函数而言，这意味着所有的极点必须位于s平面的左半开平面内。

初始值和终值定理的应用：

利用拉普拉斯变换的初值定理和终值定理可以直接从传递函数推断出系统的稳态行为。

传递函数是控制理论中的一个核心概念，广泛应用于分析和设计自动控制系统，尤其是在频域分析方面。通过传递函数，工程师们可以方便地进行系统的建模、仿真以及性能评估。

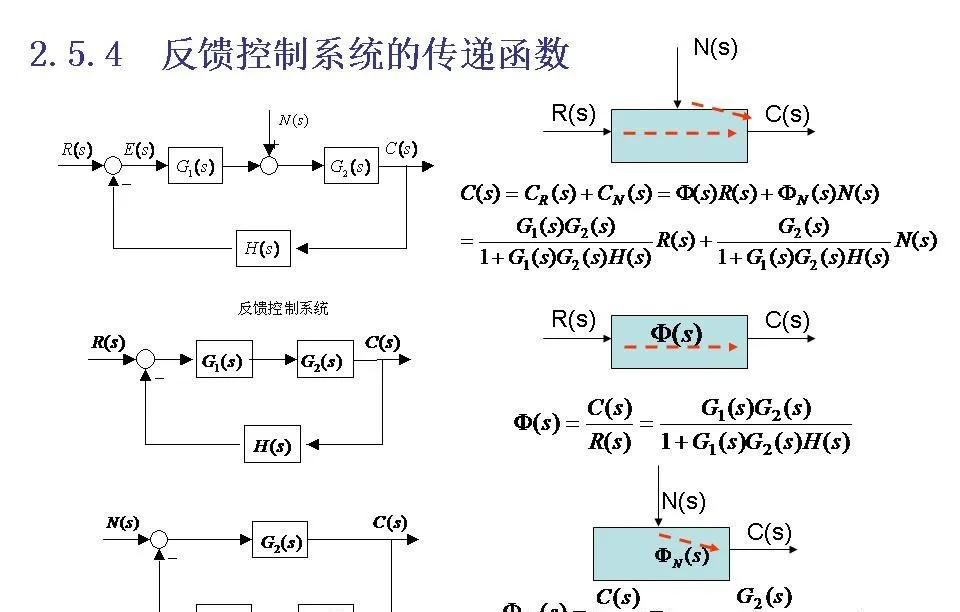
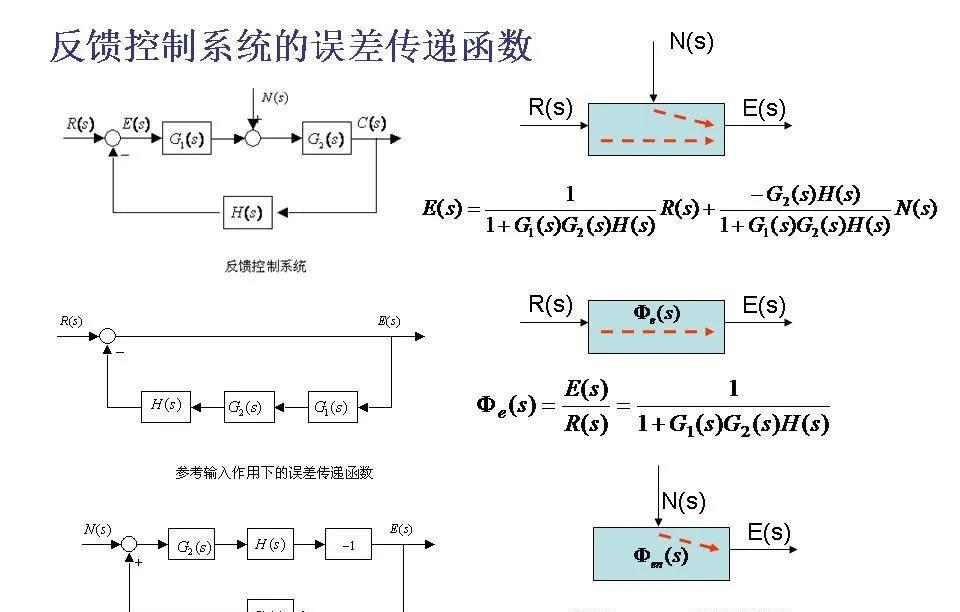
5控制系统的结构图

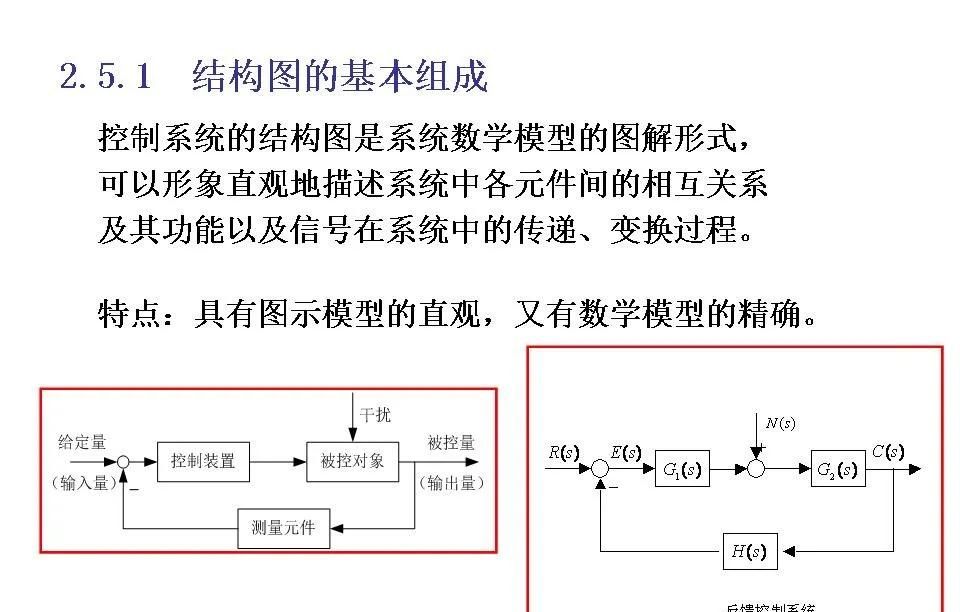
控制系统结构图（Block Diagram）是描述控制系统中各个组成部分及其相互关系的一种图形表明方法。它通过方块、箭头和节点来展示信号的流向以及系统各部分之间的连接方式，是理解和分析控制系统行为的重大工具。

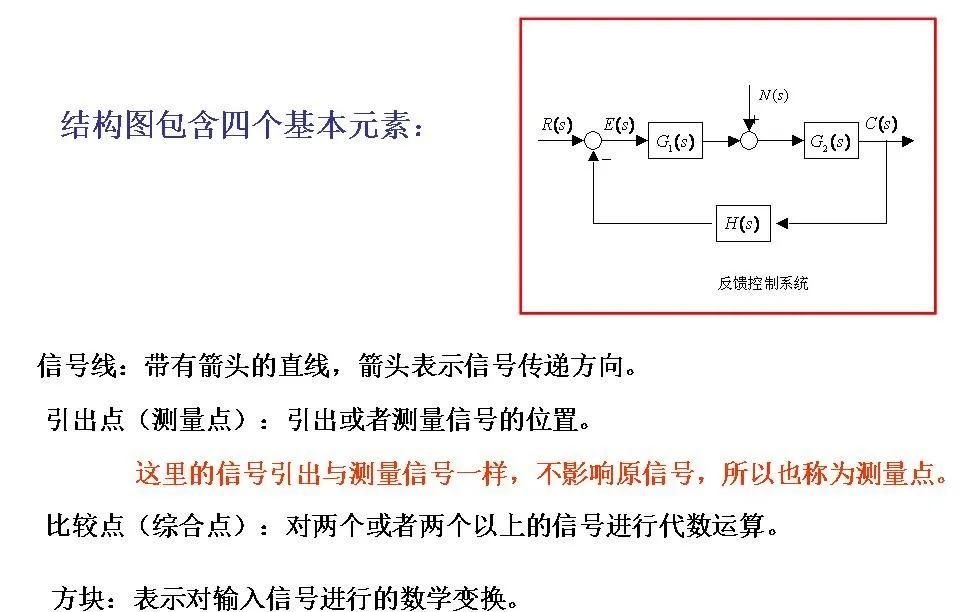
控制系统结构图的基本元素

方块（Blocks）：每个方块代表系统中的一个组件或子系统，一般内部包含传递函数，用来描述该组件对输入信号的变换作用。

箭头（Arrows）：箭头表明信号流动的方向，从输入端指向输出端。它们显示了数据在不同组件之间传输的路径。

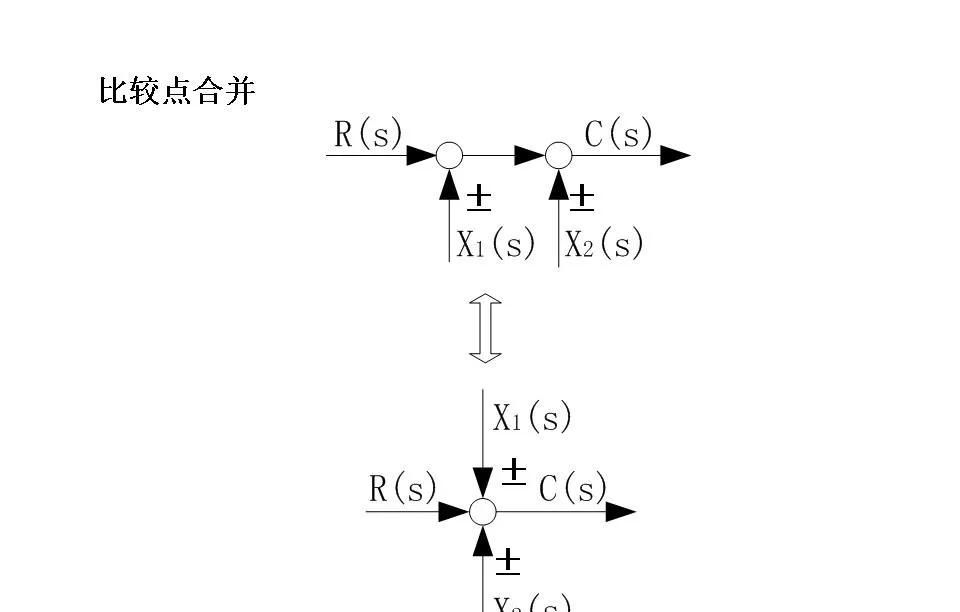
节点（Nodes）：节点是信号相交的地方，可以是加法器、减法器等运算单元，用于对多个输入信号进行组合（如求和、差分）。

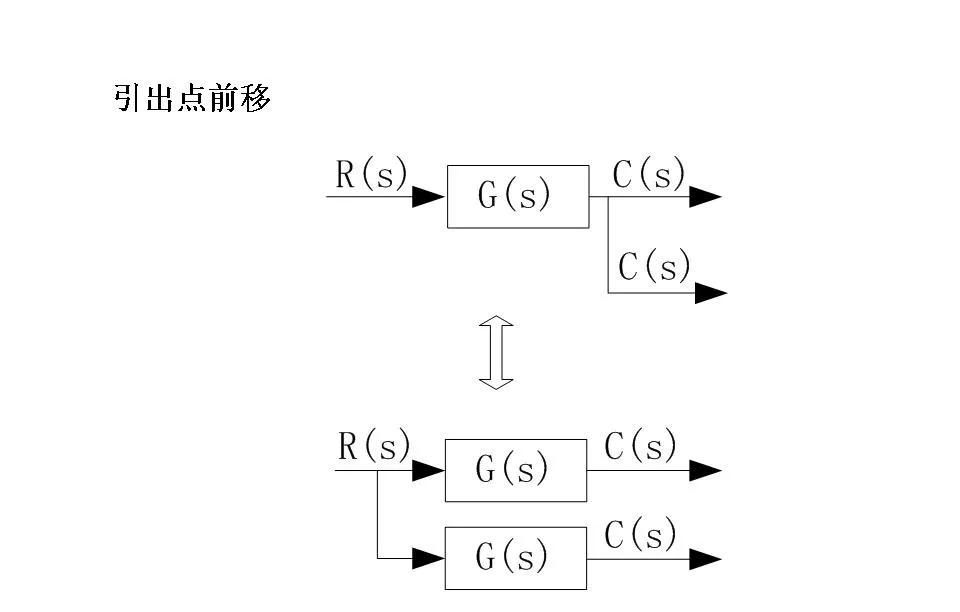
引出点（Take-off Points）：也称为分支点，用于将同一个信号分发给多个后续处理模块而不改变其值。

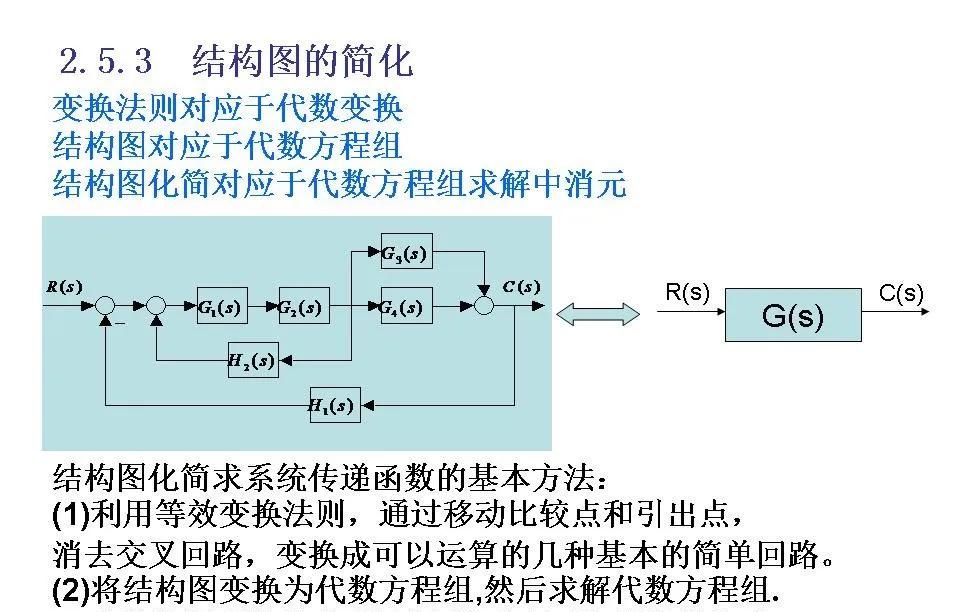
控制系统结构图化简的方法

为了简化复杂系统的结构图，使其更易于理解和分析，可以采用以下几种常见的化简技术：

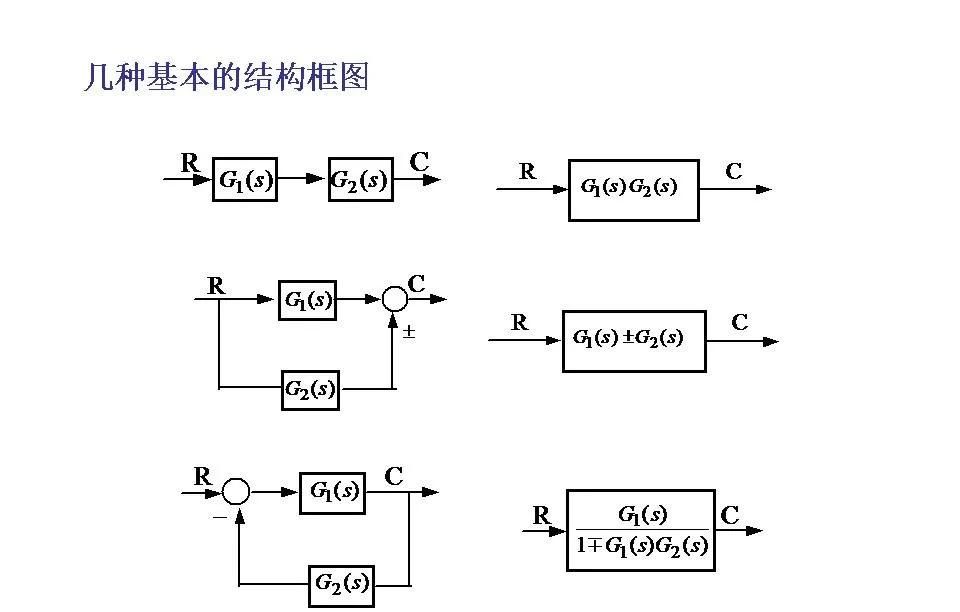
1. 相邻方块的合并

如果两个或更多个方块是串联的，即前一个方块的输出直接作为下一个方块的输入，则这些方块可以合并成一个新的单一方块，新的传递函数为原来各传递函数的乘积。

2. 并联方块的合并

对于并联的方块，如果它们共享一样的输入且输出相加，则可以用一个具有总传递函数的单一方块替代它们，总传递函数等于各个单独传递函数之和。

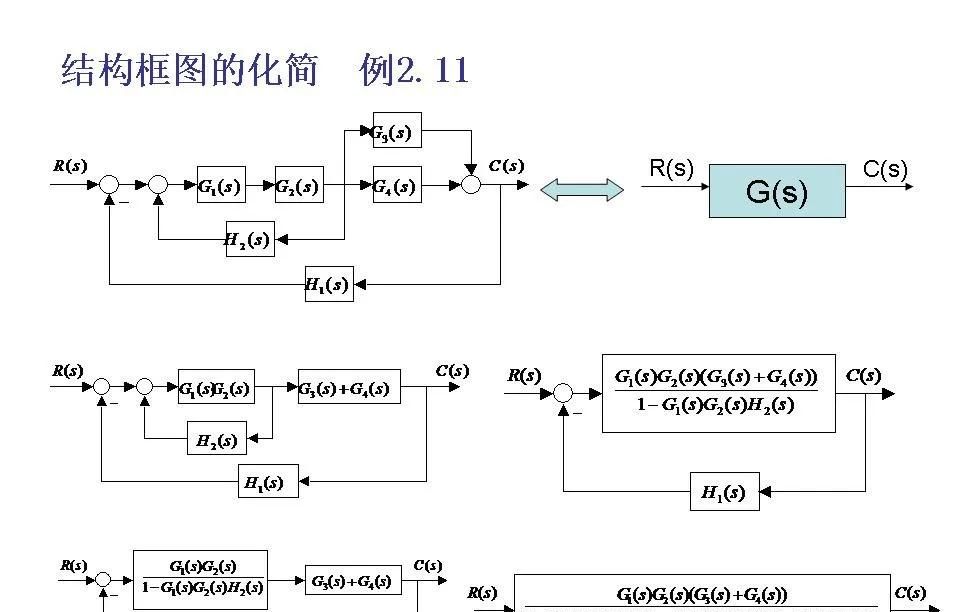
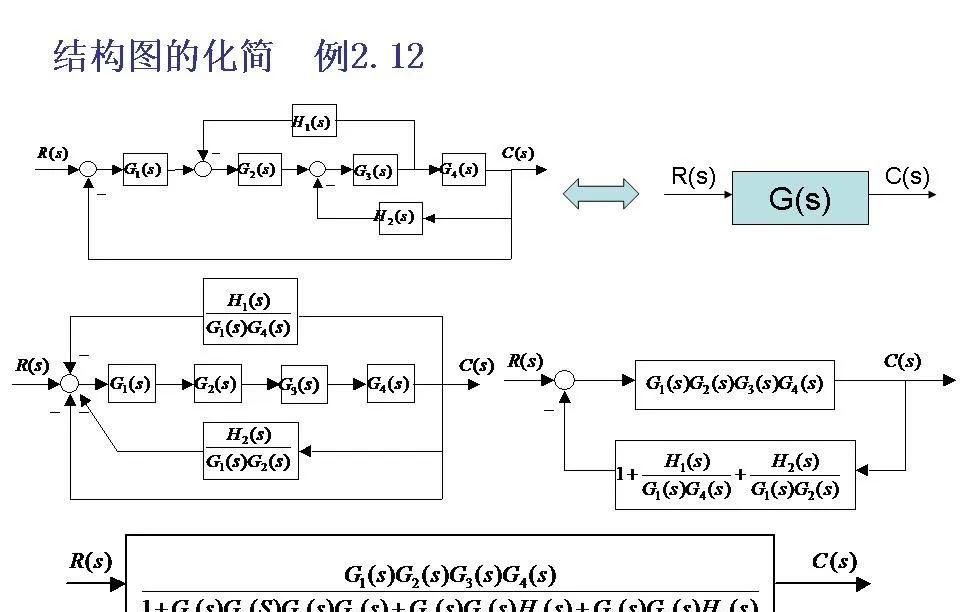
3. 反馈环路的消除

在存在反馈的情况下，可以通过应用梅森增益公式（Mason’s Gain Formula）或者直接使用标准反馈公式的简化形式来消除反馈回路，从而获得闭环传递函数。

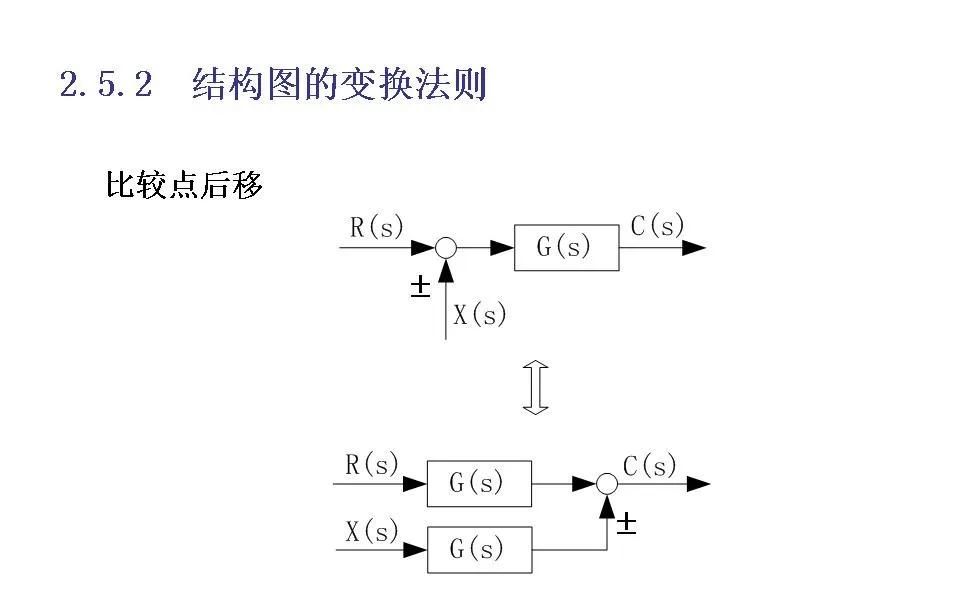
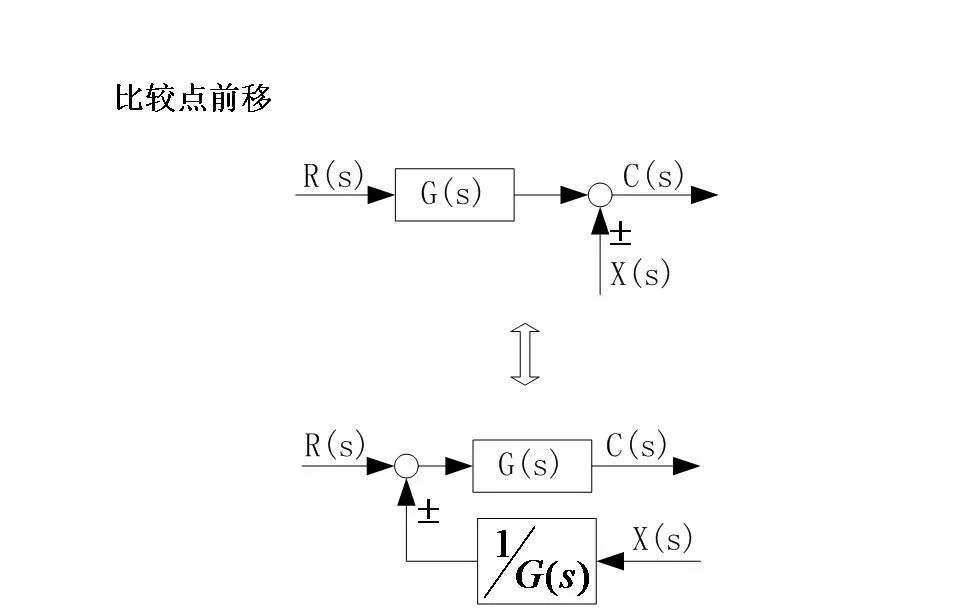
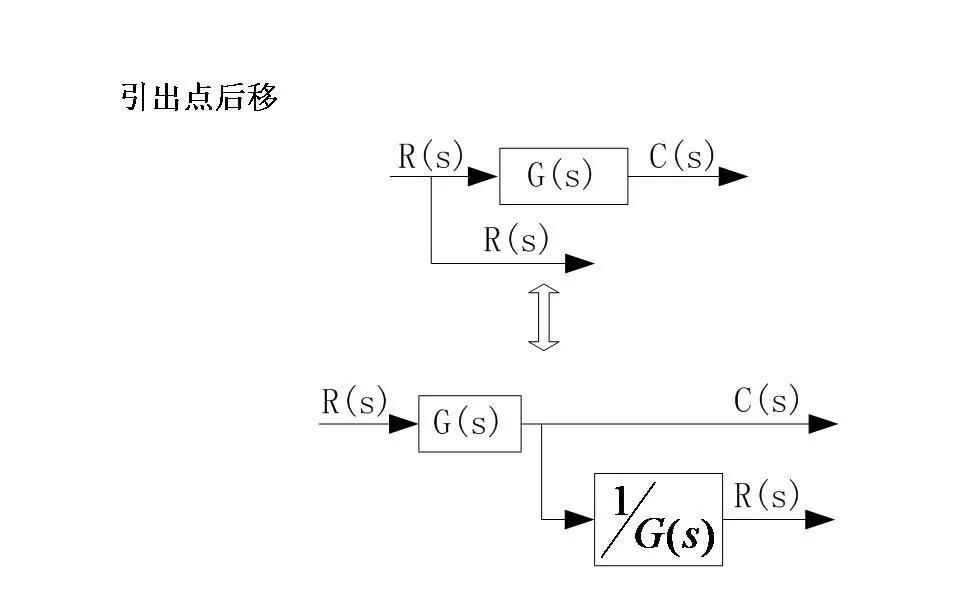
4. 移动引出点和综合点

在不改变系统功能的前提下，可以通过适当移动引出点和综合点的位置来重新排列结构图，以便更好地识别和简化其中的关系。例如，当引出点位于综合点之后时，可以将其移到综合点之前而不会影响整体特性；同样地，综合点也可以根据需要前后移动。

5. 使用梅森增益公式

当结构图超级复杂，包含多个交叉反馈路径和前向路径时，梅森增益公式提供了一种计算总体传递函数的有效方法。该公式思考了所有可能的独立前向路径以及它们与反馈路径之间的相互作用。

通过上述步骤，可以有效地简化复杂的控制系统结构图，使得问题变得更加直观，并有助于进一步的数学分析和设计优化。在实际操作中，可能会结合多种方法来进行逐步化简，直到得到最简洁的形式。